算法学习记录

本文最后更新于：3 个月前

算法学习记录

本文档按照时间 记录了笔者写算法题的随笔

更多题解分享与思路交流可移步笔者leetcode主页：https://leetcode.cn/u/dutsc/

十一假期

子序列，子串类型的动态规划

滑动窗口

HashSet

优先队列（堆，可传比较器）

单调队列（滑动窗口的最大值）（用双端队列实现Deuqe）

用map统计元素出现的频率 map.put(num,map.getOrDefault(num,0)+1);

往优先队列中传入比较器，注意比较器也要有泛型(使用匿名内部类)

1
2
3
4
5
6
7
8
9
10
Queue<Map.Entry<Integer,Integer>> pq = new PriorityQueue<>(new Comparator<Map.Entry<Integer,Integer>>(){
    public int compare(Map.Entry<Integer,Integer> e1,Map.Entry<Integer,Integer> e2){
        return e1.getValue() - e2.getValue();
    }
});
//Map.Entry中第一个存放num数值，第二个存放num出现的频率。
//优先队列实现一个小顶堆，按照出现的频率排序
// 完全可以使用数组int[]代替

//若存入优先队列的值是Double类型，需要使用内置的Double.compare()方法来作为compare的返回值

编辑距离 dp

10/8

优先队列题目优化，改用大顶堆，找到出现频率前k高的元素然后再poll

lambda表达式的写法，比比较器方便

深度优先搜索 dfs ‘X’ ‘O’变化 标记法

集合的时间复杂度

  • ArrayList 查 O（1） 增 末尾0（1）中间0（n） 删0（n）

  • LinkedList 查 O（n） 增 末尾0（1）中间0（n） 删0（1）
    因为增加到中间，要先查询到增加的位置，故增加到中间时间复杂度为O(n)

  • Set集合有三个常见的实现类：HashSet，TreeSet，LinkedHashSet。
    简单的说，如果你关注性能，应该使用HashSet；
    如果你需要一个有序的Set集合，应该使用TreeSet；
    如果你需要一个Set集合保存了原始的元素插入顺序，应该使用LinkedHashSet。

    • HashSet 是基于散列表实现的，元素没有顺序；add、remove、contains方法的时间复杂度为O(1)。(contains为false时，就直接往集合里存)
      总结：查 0（1） 增 0（1） 删0（1）

    • TreeSet是基于树实现的（红黑树），元素是有序的；add、remove、contains方法的时间复杂度为O(log (n))(contains为false时，插入前需要重新排序)。

      总结：查 0（log n） 增 0（log n） 删0（log n）

    • LinkedHashSet介于HashSet和TreeSet之间，是基于哈希表和链表实现的，支持元素的插入顺序；基本方法的时间复杂度为O(1)；

      待定
      总结：查 0（1） 增 0（1） 删0（1）

  • map集合有三个常见的实现类：HashMap，TreeMap，LinkedHashMap。

    • TreeMap基于红黑树（一种自平衡二叉查找树）实现的，时间复杂度平均能达到O(log n)。
    • HashMap是基于散列表实现的，时间复杂度平均能达到O(1)。正常是0(1)到0（n） jdk1.8添加了 红黑树 是 0（log n）
    • TreeMap的get操作的时间复杂度是O(log(n))的，相比于HashMap的O(1)还是差不少的。
    • LinkedHashMap的出现就是为了平衡这些因素，能以O(1)时间复杂度查找元素，又能够保证key的有序性

10/9

并查集基础题

并查集困难题，应用没做出来？？

每日一题，不会做

10/13

做了一些基础的模拟题，贪心题

String的valueOf方法 将基本数据类型转换成字符串型的方法

String 类别中已经提供了将基本数据型态转换成 String 的 static 方法 ，也就是 String.valueOf() 这个参数多载的方法

拓展：将String转为基本数据类型

要将 String 转换成基本数据型态转 ，大多需要使用基本数据型态的包装类别

　　比如说 String 转换成 byte ，可以使用 Byte.parseByte(String s) ，这一类的方法如果无法将 s 分析 则会丢出 NumberFormatException

（1）byte : Byte.parseByte(String s) : 将 s 转换成 byte

（2）Byte.parseByte(String s, int radix) : 以 radix 为基底 将 s 转换为 byte ，比如说 Byte.parseByte(“11”, 16) 会得到 17

（3）double : Double.parseDouble(String s) : 将 s 转换成 double

（4）float : Double.parseFloat(String s) : 将 s 转换成 float

（5）int : Integer.parseInt(String s) : 将 s 转换成 int

（6）long : Long.parseLong(String s)

上述方法都可以忽略字符串中的前导0，直接转化为去除前导零的数字

putIfAbsent(k,v)

如果key不为空，就不插入新值了

若key不为空，则返回旧的value；若key为空，则返回null（返回旧的value）

computeIfAbsent

putIfAbsent()中没有计算方法，直接给出value，而computeIfAbsent()中可以有value的计算方法（函数），也可以使用lambda表达式

java8之前。从map中根据key获取value操作可能会有下面的操作

1
2
3
4
5
Object key = map.get("key");
if (key == null) {
    key = new Object();
    map.put("key", key);
}

java8之后。上面的操作可以简化为一行，若key对应的value为空，会将第二个参数的返回值存入并返回

1
Object key2 = map.computeIfAbsent("key", k -> new Object());

如果v已经计算好了，那么适合使用putIfAbsent(k, v)，如果v还未计算，同时计算需要一些耗时,那么建议使用computeIfAbsent，将获取v值的计算放到lambada表达式体内，这样只有再map不含有k对应值时才会进行获取v值的计算，可以优化性能

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
public class MapInfo {
 
    public static void computeIfAbsent(){ // jdk1.8新特性哦
        HashMap<String> map = new HashMap&lt;>();
        map.put("1","is map");
        map.put("2","contains a mapping");
        map.put("3","specified");
        map.put("4","inappropriate");
        map.computeIfAbsent("5", MapInfo::apply);
        System.out.println(map.get("5"));
    }
 
    private static Object apply(String v) {
        return v = "is 5";
    }
}

10/16

720.词典中最长的单词

注意：

  1. 注意返回值为String，返回null是不对的，若为null应该返回””
  2. 只找最大或最小的值，考虑优先队列存储，传入比较器

10/18

移位运算符

根据这个规则，左移32位后，右边补上32个0值是不是就变成了十进制的0了？答案是NO，当int类型进行左移操作时，左移位数大于等于32位操作时，会先求余（%）后再进行左移操作。也就是说左移32位相当于不进行移位操作，左移40位相当于左移8位（40%32=8）。当long类型进行左移操作时，long类型在二进制中的体现是64位的，因此求余操作的基数也变成了64，也就是说左移64位相当于没有移位，左移72位相当于左移8位（72%64=8）
注意：其它几种整形byte，short移位前会先转换为int类型（32位）再进行移位

和左移一样，int类型移位大于等于32位时，long类型大于等于64位时，会先做求余处理再位移处理，byte，short移位前会先转换为int类型（32位）再进行移位。以上是正数的位移，我们再来看看负数的右移运算，

无符号移位>>>

无符号右移运算符>>>和右移运算符>>是一样的，只不过右移时左边是补上符号位，而无符号右移运算符是补上0，也就是说，对于正数移位来说等同于：>>，负数通过此移位运算符能移位成正数。

在不大于自身数值类型最大位数的移位时，一个数左移n位，就是将这个数乘以2的n次幂；一个数右移n位，就是将这个数除2的n次幂，然后取整。
比如int32位的（64位也是同样方法）：

1
2
7 >> 1  = 7/2  取整为3
7 << 1  = 7*2  为14

如果移动位数超过了32位怎么办？把移位数和32取余数得到的数字套用即可：

如 9 >> 67
1、先67对32取余，结果是3
2、然后9/8 得到结果为1

实验

C艹里面1最大左移31位，变成最小负数，然后这个数不能再-1

java

10/20

Tree的bfs与图的bfs的区别

相信对于Tree的BFS大家都已经轻车熟路了：要把root节点先入队，然后再一层一层的无脑遍历就行了。

对于图的BFS也是一样滴～ 与Tree的BFS区别如下：
1、tree只有1个root，而图可以有多个源点，所以首先需要把多个源点都入队。
2、tree是有向的因此不需要标志是否访问过，而对于无向图来说，必须得标志是否访问过！
并且为了防止某个节点多次入队，需要在入队之前就将其设置成已访问！

图的bfs遍历时，需要创建一个used数组来标记某个节点是否已经入队。已经入队的节点标记为true，将某个节点入队之前先判断它是否已经被访问过，若没有被访问过再入队。

入队之前判断，这样可以保证一个节点不会重复入队。

1162.地图分析

这是一道典型的BFS基础应用，为什么这么说呢？
因为我们只要先把所有的陆地都入队，然后从各个陆地同时开始一层一层的向海洋扩散，那么最后扩散到的海洋就是最远的海洋！
并且这个海洋肯定是被离他最近的陆地给扩散到的！

拓扑排序

课程表题目210 207 给出课程学习的拓扑排序，利用BFS

c++map的性质

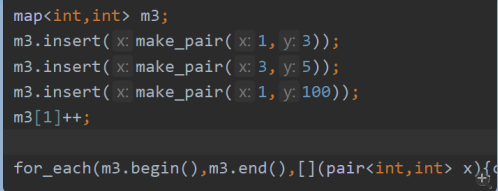
cpp中map的性质

输出1 4 3 5

若key与之前的key相等，则不会替换之前的map

map可以通过m3[1]直接获取key为1的value值，并且通过++来使value+1

10/26

拓扑排序+动态规划 类型的困难题 1857

快速获取数组中的最大值最小值的方法：

Java

1
Arrays.stream(nums).max().getAsInt();

C++

1
2
*max_element(array,array+n);
int myMax = *min_element(arr.begin(),arr.end());//也可以

10/28

判断一个数是不是2的整数次幂

1
if(!num&(num-1)) return true;

此操作，翻转了num最右边的1

c++将数字转化为字符串

1
to_string();

将字符串转化为数字

1
2
3
4
5
#include <stdio.h>
#include <stdlib.h>

atoi;//string to int   可以直接忽略前导0  超过上下界输出上下界
atof;//string to float

11/2

只知道当前节点，想要删除当前节点的方法：

不可取的设计模式！ 本质上来说，单链表节点无法做到在链表里删除自身

1
2
3
4
5
6
7
8
//只适用于Java，因为Java有垃圾回收器GC
if(node.next!=null){
    node.val = node.next.val;
    node.next = node.next.next;
}
else{
    node = null;
}

lambda表达式中的差值，若是long类型，则必须转换为 int类型，否则会报错。因为compare方法返回的是int类型，要想不强转，只能重写compare方法

1
2
long[][] dp = new long[2][n];
PriorityQueue<long[]> minHeap = new PriorityQueue<>((a,b)->a[1]-b[1]);

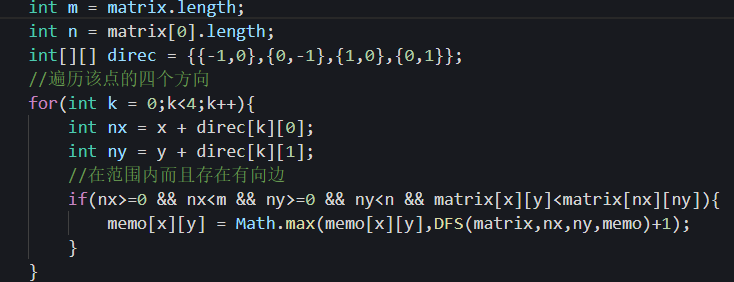
11/3

取出一个点，一次遍历它的上下左右的技巧：

遍历一个矩阵中上下左右四个位置

11/11

记忆化深度优先搜索：

当发现DFS出现大量重复计算时，若是矩阵，则可以创建一个缓存矩阵，来存储其已经遍历到的结果，这样就可以不用每次DFS的时候都要重新遍历了。

省下used数组空间的小技巧：

329.矩阵中的最长递增路径 一题中，memo矩阵存储从该点开始DFS的最长路径，将其初始值置为0，这样在遍历过程中，若$memo[i][j]$是0，就可以认为该位置没有被遍历过，就要重新遍历；

若$memo[i][j]$ 不是0，则直接返回该点的值即可，不需要再重新遍历。

11/16

判断连接成完美矩形的条件：

  • 左下，右上，右下，左上的点只出现一次，其他的点成对出现
    于是这就有了思路：若某一节点不在哈希表中，则加入，若已经在哈希表中，则删除，最后判断哈希表中元素个数是否为4，而且是左下，右上，右下，左上四个节点
  • 每个矩形面积的累加和，看是不是等于最大的右上值减去最小的左下值，相等则true，不相等则false

这里有一个小技巧：判断矩形的某一个点是已经存在。

由于矩形的点是用一个二元组来表示的，常规想法不太好存储，有一个小妙招：Set中存储 ，将矩形每个点的坐标拼接起来，这个String就代表该点的坐标，只需要判断该String是否在哈希表中即可。

非常巧妙的变二维为一维的思想！

11/17

c++中，size() 和 length() 返回值类型是无符号数unsigned，若需要转为int类型则需要调用强制类型转换函数

11/22

java数组的clone方法

A.一维数组：深克隆（重新分配空间，并将元素复制过去）

对clone后的数组进行修改不会影响源数组。
B.二维数组：浅克隆（只传递引用）

对clone后的数组进行修改时，将对源数组也产生影响（因为复制的是引用，实际上指向的是同一个地址）

实现二维数组的深克隆

1
2
3
4
5
int[][] a={{3,1,4,2,5},{4,2}};
int[][] b=new int[a.length][];
for(int i=0;i<a.length;i++){
        b[i]=a[i].clone();
}

11/28

筛法求素数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int n;
Scanner sc = new Scanner(System.in);
n = sc.nextInt();
int[] arr = new int[n];
for (int i = 2; i < n; i++) {
    arr[i] = i;
}
for (int i = 2; i < n; i++) {
    if (arr[i] != 0) {
        int j, temp;
        temp = arr[i];
        for (j = 2 * temp; j < n; j = j + temp) { //这一步可以直接从temp[i]*temp[i]开始进行查找，可以证明
            arr[j] = 0;
        }
        System.out.print(arr[i] + " ");
    }
}

下标就是其值

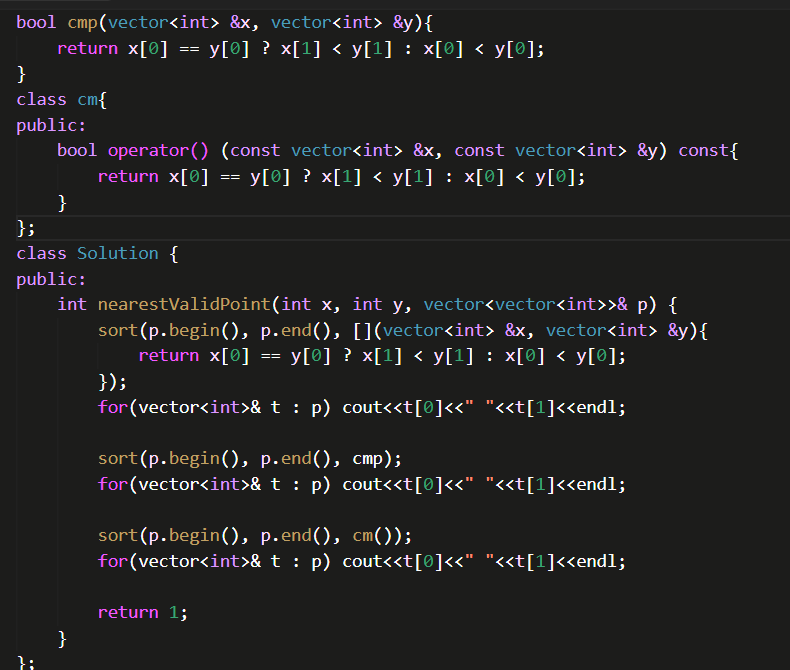
11/29

c++优先队列自定义排序

优先队列使用仿函数，仿函数后面不加()，sort中使用仿函数，必须要加()；sort使用普通函数，必须使用static的函数，

1
2
3
4
5
6
public:
    static bool cmp(int &a,int &b){
        return a>b;
    }

 sort(candidates.begin(),candidates.end(),cmp);

注意：

  1. 若有两个数，使用pair比使用vector快得多

  2. 使用emplace比push快，push要加上{}，emplace不用，直接写两个数就可以

  3. priority_queue的排序返回值类型是bool，不是int 注意！！而且，> 前者>后者是从小到大排序，< 前者<后者是从大到小排序 ，优先队列使用仿函数排序，不能加()；使用普通函数排序，必须是static，而且必须使用函数指针（*暂时还没有研究）

  4. sort排序顺序与java中的相同，与priority_queue相反，< 表示从小到大排序，>表示从大到小排序。sort使用仿函数必须加()，sort使用普通函数不加()，但是普通函数必须是static的

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
class cmpo{
    public:
    bool operator()(pair<int,int> &x,pair<int,int> &y){
        return x.first*y.second>x.second*y.first;
    }
};

// class cmpv{
//     public:
//     bool operator()(vector<int> &x,vector<int> &y){
//         return x[0]*y[1]>x[1]*y[0];
//     }
// };

class Solution {
public:
    // bool cmp(pair<int,int> x,pair<int,int> y){
    //     return x.first*y.second-x.second*y.first;
    // }
    vector<int> kthSmallestPrimeFraction(vector<int>& arr, int k) {
        int n = arr.size();
        priority_queue<pair<int,int>,vector<pair<int,int> >,cmpo> minHeap;
        // priority_queue<vector<int>,vector<vector<int>>,cmpv> minHeap;
        for(int i = 0;i<n;i++){
            for(int j = i+1;j<n;j++){
                // minHeap.push({arr[i],arr[j]});
                minHeap.emplace(arr[i],arr[j]);
            }
        }
        int len = minHeap.size();
        pair<int,int> temp;
        // vector<int> temp; 
        for(int i = 0;i<len;++i){
            if(i==k-1){
                temp = minHeap.top();
                break;
            }
            // pair<int,int> t = minHeap.top();
            // cout << t.first << " " << t.second << endl;
            minHeap.pop();
        }
        vector<int> a;
        a.push_back(temp.first);
        a.push_back(temp.second);
        // a.push_back(temp[0]);
        // a.push_back(temp[1]);
        return a;
    }
};

c++排序方法：

cpp排序方法

2022 1/8

java中可以使用path.split(“/“)将字符串path使用/进行分割，并返回一个字符串数组。

1
String[] names = path.split("/");

中间有不定数量空格隔开的字符串，也能分割成字符串数组

1
2
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String[] tt = br.readLine().split(" +");

背包问题

01背包

若采用先遍历物品，再遍历背包容量的方式，背包容量要从大到小遍历

完全背包

遍历顺序与01背包不同，若采用先遍历物品，再遍历背包容量的方式，背包容量要从小到大遍历，这样每一个物品都可以无限次被拿取。

求一共有多少种零钱组合金额的题目，就是求有多少种物品放入背包的方式，递推公式一般为$dp[i] += dp[i-cost[i]]$ ，而且注意，$dp[0]$ 一定要初始化为1，否则后面都是0，没有意义。

==for循环的遍历顺序与 是 组合还是排列 有关系！==

  1. 先遍历物品（钱币金额），再遍历背包容量（金钱总额），求的是组合数
  2. 先遍历背包容量（金钱总额），再遍历物品（钱币金额），求的是排列数。

滚动数组中，倒序遍历是为了保证每个物品只被添加一次

子序列问题

子序列默认不连续，子数组默认连续

最长递增子序列（LIS）

对于每一个位置，依次遍历该位置之前的所有位置，求得最长递增子序列的长度，然后再加一

on2

Ologn的解法

利用贪心和二分的思想，维护一个最长自增子序列数组d，若a[i] < d[len] ，则在d数组中二分查找第一个小于a[i] 的元素，在他的下一个位置将d数组中的元素替换成a[i] ，

这是因为，总是想让最长上升子序列上升的最慢。len的值(index+1) 就是最长递增子序列的长度。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
class Solution {
    int[] d;
    public int lengthOfLIS(int[] nums) {
        int n = nums.length;
        if(n==1) return 1;
        d = new int[n];
        d[0] = nums[0];
        int index = 0;
        for(int i = 1;i<n;++i){
            if(nums[i]>d[index]){
                d[++index] = nums[i];
            }else if(nums[i]==d[index]) continue;
            else{
                int id = binarySearch(0,index,d,nums[i]);
                d[id] = nums[i];
            }
        }
        return index+1;
    }
    int binarySearch(int l,int r,int[] d,int target){
        while(l<r){
            int mid = ((r-l)>>1)+l;
            if(d[mid]>=target) r = mid;
            else l = mid+1;
        }
        return r;
    }
}

最长连续递增子序列

因为要求连续递增子序列，所以就不需要比较$dp[i]$和$dp[j] (j<i)$ ，而是直接比较$dp[i+1]$ 和$dp[i]$ ，故只需要一层for循环即可。

区别：

  • 不连续的子序列，跟之前的所有状态都有关（0-i个状态）
  • 连续的子序列，只跟前一个状态有关。

最长重复子数组

最长公共子序列（LCS）

1/23

辗转相除法求最大公约数

1
2
3
4
5
6
7
8
int GCD(int a, int b)
{
    if (a%b == 0)
    {
        return b;
    }
    return GCD(b, a%b);
}

最小公倍数

1
2
3
int LCM(int a,int b){
    return a/GCD(a,b)*b;
}

1/24

Manacher算法

马拉车算法

Manacher 算法是在线性时间内求解最长回文子串的算法。

算法要点：

image-20220124140113642

  1. 奇偶统一判断：在每一个字符中间加入一个本字符串中没有出现过的字符（首尾也加）

    转换之后，所有的回文串长度都是奇数

    对于以$T[i]$ 为中心的最长回文子串，其长度为$2\times L[i]-1$ (带#)

    可以证明，$Len$ 数组可以求出，$Len(i)$ 表示以下标为i的字符为中心，最长回文子串的长度为$Len(i)-1$ .原问题就转化为求$Len(i)$ （每一个字符的回文半径）

求最长回文子串

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
class Solution {
    public String addString(String s){
        StringBuilder sb = new StringBuilder("#");
        for(int i = 0;i<s.length();++i){
            sb.append(s.charAt(i));
            sb.append('#');
        }
        return sb.toString();
    }
    public String longestPalindrome(String s) {
        int n = s.length();
        if(s.length()<2){
            return s;
        }
        s = addString(s);
        int mx = 0;
        int loc = 0;
        int mymax = 0;
        int start = 0;
        int[] p = new int[2*n+1];
        for(int i = 0;i<2*n+1;++i){
            if(mx-i>0 && 2*loc-i>=0){
                p[i] = Math.min(mx-i,p[2*loc-i]);
            }
            else p[i] = 1;
            while(i+p[i]<2*n+1 && i-p[i]>=0 && s.charAt(i+p[i])==s.charAt(i-p[i])){
                p[i]++;
            }
            if(i+p[i]>mx){
                mx = i+p[i];
                loc = i;
            }
            if(mymax<p[i]){
                mymax = p[i];
                start = i;
            }
        }
        String t = s.substring(start-p[start]+1,start+p[start]);
        StringBuilder sb = new StringBuilder();
        for(int i = 0;i<t.length();++i){
            if(t.charAt(i)=='#'){
                continue;
            }
            sb.append(t.charAt(i));
        }
        return sb.toString();
    }
}

求回文串的个数（把加上#的数组中，每一个p[i]的值/2并累加）为什么？？？ 好像懂了

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
class Solution {
    public String addString(String s){
        StringBuilder sb = new StringBuilder();
        sb.append('#');
        int n = s.length();
        for(int i = 0;i<n;++i){
            sb.append(s.charAt(i));
            sb.append('#');
        }
        return sb.toString();
    }
    public int countSubstrings(String s) {
        if(s.length()<2){
            return 1;
        }
        s = addString(s);
        // System.out.println(s);
        int n = s.length();
        int mx = 0,loc = 0;
        int[] p = new int[n];
        char[] c = s.toCharArray();
        for(int i = 0;i<n;++i){
            if(mx>i && 2*loc-i>=0){
                p[i] = Math.min(mx-i,p[2*loc-i]);
            }
            else{
                p[i] = 1;
            }
            while(i+p[i]<s.length()&&i-p[i]>=0 && c[i+p[i]]==c[i-p[i]]){
                p[i]++;
            }
            if(i+p[i]>mx){
                mx = i+p[i];
                loc = i;
            }
        }
        int sum = 0;
        for(int i = 0;i<p.length;++i){
            sum+=p[i]/2;
            // System.out.println(p[i]);
        }
        return sum;
    }
}

唯一一个疑点：为什么取最小值？

1/26

线段树

查询方法：

  1. 如果这个区间被完全包括在目标区间里里面，直接返回这个区间的值
  2. 如果这个区间的左儿子和目标区间有交集，那么搜索左儿子
  3. 如果这个区间的右儿子和目标区间有交集，那么搜索右儿子

那么对于区间操作，我们考虑引入一个名叫“lazy tag 懒标记）的东西——之所以称其“lazy”，是因为原本区间修改需要通过先改变叶子节点的值，然后不断地向上递归修改祖先节点直至到达根节点，时间复杂度最高可以到达O(nlogn)的级别。但当我们引入了懒标记之后，区间更新的期望复杂度就降到了O(log**n)的级别且甚至会更低.

懒标记

pushdown都是在区间分裂之前进行

懒标记的作用是，记录每次，每个结点要更新的值。 但线段树的优点不在于全记录，而是传递式记录：

整个区间都被操作，记录在公共祖先节点上，只修改了一部分，就只记录在这部分的公共祖先上，如果只修改了自己的话，就只改变自己。

懒标记的意义

由于我们要做的操作是区间加一个数，所以我们不妨在区间进行修改时为该区间打上一个标记，就不必再修改他的儿子所维护区间，等到要使用该节点的儿子节点维护的值时，再将懒标记下放即可，可以节省很多时间，对于每次区间修改和查询，将懒标记下传，可以节省很多时间

注意：也是第一次写代码一直不通过的原因：

  1. 用线段树维护不同的情况（如区间和，区间最大值），pushdown的逻辑会稍有变化。
    若是维护区间最值，第一种情况就是tree的区间是[l,r]的子集
    若是维护区间和，第一种情况就是tree的区间与[l,r]相等
  2. 查询query和更新update时，要查询的l r不要变，只改变lc，rc就好
  3. build时，要查询的l r都要变，lc rc也要变

L,R是要查询的区间的范围

区间都乘某个数

若是区间乘法，（洛谷模板题2）则要设两个懒标记，一个lazyAdd，一个lazyMul。

乘法操作时，lazyMul*=k lazy+=k

加法操作时 lazyMul不变 lazyAdd+=k

注意

区间修改
  1. 如果整个区间都被包含就修改整个区间，否则分裂区间，递归处理子区间后再回溯处理父节点代表的区间。
  2. 懒标记：如果每次递归处理到叶子节点，复杂度不行，付姐带你表示的区间是左右儿子的整合，我修改父节点表示的区间，因为打了标记，我就会把以前的修改顺带做了，并且把懒标记传递下去。
java对象数组特点

  1. 对于对象数组，使用运算符new只是为数组本身分配空间，并没有对数组的元素进行初始化。即数组元素都为空，
    对象数组初始化

    正确的使用方法，应该分别对每个对象进行初始化，并且不能使用增强for循环，因为增强for循环不是本体。

  2. 对于基本数据类型，采用new初始化数组时，数组元素也进行了相应的初始化

带懒标记的线段树模板

Java版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
class Node{
    int l;
    int r;
    int add;
    int sum;
//    int mul;
    Node(int _l,int _r){
        this.l = _l;
        this.r = _r;
    }
    Node(){

    }
}

public class SegmentTreePushdown {
    static int[] nums;
    static Node[] tree;
    static int n;
    public static void main(String[] args) {
        int[] _nums = {1,3,5,7,9,11};
        nums = _nums;
        int n = nums.length;
        tree = new Node[4*n];
        for(int i = 0;i<4*n;++i){
            tree[i] = new Node();
        }
        build(1,0,n-1);
        for(Node tt:tree){
            System.out.println(tt.l + " " + tt.r + " " + tt.sum);
        }
        update(1,2,5,3);
        int sumtt = query(1,1,4);
        System.out.println(sumtt);
    }

    // 建树
    static void build(int node, int start, int end){
        tree[node].l = start;
        tree[node].r = end;
        if(start==end){
            tree[node].sum = nums[start];
            return ;
        }
        int mid = ((end-start)>>1)+start;
        build(node<<1,start,mid);
        build(node<<1|1,mid+1,end);
        pushup(node);
    }
    // 区间更新
    static void update(int node,int L, int R, int val){
        System.out.println(1);
        if(L<=tree[node].l && R>=tree[node].r){
            tree[node].add += val;
            tree[node].sum += val*(tree[node].r-tree[node].l+1);
            return ;
        }
        int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
        pushdown(node);
        if(L<=mid)
            update(node<<1,L,R,val);
        if(R>mid)
            update(node<<1|1,L,R,val);
        pushup(node);
    }
    // 区间查询
    static int query(int node, int L,int R){
        if(L>tree[node].r || R<tree[node].l) return 0;
        if(L<=tree[node].l && R>=tree[node].r) return tree[node].sum;
        pushdown(node);
        int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
        int res = 0;
        if(L<=mid)
            res += query(node<<1,L,R);
        if(R>mid)
            res += query(node<<1|1,L,R);
        return res;
    }
    // 回溯更新
    static void pushup(int node){
        tree[node].sum = tree[node<<1].sum+tree[node<<1|1].sum;
    }
    // 下传懒标记
    static void pushdown(int node){
        if(tree[node].add!=0){
            tree[node<<1].add += tree[node].add;
            tree[node<<1].sum += tree[node].add*(tree[node<<1].r-tree[node<<1].l+1);
            tree[node<<1|1].add += tree[node].add;
            tree[node<<1|1].sum += tree[node].add*(tree[node<<1|1].r-tree[node<<1|1].l+1);
            tree[node].add = 0;
        }
    }
}

这份代码第一次写，出错的地方：

  1. update 和query 在判断递归条件的时候，要用L R和mid作比较，而不是用tree的lr。
  2. pushdown操作中，子节点的懒标记要使用+=，而不是直接赋值。因为可能子节点之前就有懒标记了。

c++版本

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
//
// Created by s'c on 2022/4/4.
//
#include "iostream"
using namespace std;
typedef long long ll;
const int MAX = 100010;
int nums[MAX]={0};
struct node{
    int l;
    int r;
    ll add;
    ll sum;
};
node tree[4*MAX];

void pushup(int node){
    tree[node].sum = tree[node<<1].sum + tree[node<<1|1].sum;
}
void build(int node,int l,int r){
    tree[node].l = l;
    tree[node].r = r;
    if(l==r){
        tree[node].sum = nums[l];
        return ;
    }
    int mid = ((r-l)>>1)+l;
    build(node<<1,l,mid);
    build(node<<1|1,mid+1,r);
    pushup(node);
}

void pushdown(int node){
    if(tree[node].add){
        tree[node<<1].add += tree[node].add;
        tree[node<<1|1].add += tree[node].add;
        tree[node<<1].sum += tree[node].add*(tree[node<<1].r-tree[node<<1].l+1);
        tree[node<<1|1].sum += tree[node].add*(tree[node<<1|1].r-tree[node<<1|1].l+1);
        tree[node].add = 0;
    }
}

void update(int node,int L,int R,int val){
    if(L<=tree[node].l && R>=tree[node].r){
        tree[node].sum += val*(tree[node].r-tree[node].l+1);
        tree[node].add += val;
        return;
    }
    int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
    pushdown(node);
    if(L<=mid) update(node<<1,L,R,val);
    if(R>mid) update(node<<1|1,L,R,val);
    pushup(node);
}
ll query(int node,int L,int R){
    if(R<tree[node].l || L>tree[node].r) return 0;
    if(L<=tree[node].l && R>=tree[node].r) return tree[node].sum;
    int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
    pushdown(node);
    ll res = 0;
    if(L<=mid) res+=query(node<<1,L,R);
    if(R>mid) res+=query(node<<1|1,L,R);
    return res;
}

int main(){
    int n,m;
    scanf("%d%d",&n,&m);
    for(int i = 0;i<n;++i){
        scanf("%d",&nums[i]);
    }
    build(1,0,n-1);
    while(m-->0){
        int tt;
        scanf("%d",&tt);
        if(tt==1){
            // update
            int l,r,k;
            scanf("%d%d%d",&l,&r,&k);
            update(1,l-1,r-1,k);
        }else{
            // query
            int l,r;
            scanf("%d%d",&l,&r);
            ll ans = query(1,l-1,r-1);
            printf("%ld\n",ans);
        }
    }
}

树状数组

区间长度

$c[i]$ 存储的值的区间长度为$lowbit(i)$ 则$lowbit(i)=(-i)&i$

前驱和后继

$c[i]$ 的直接前驱为$c[i-lowbit(i)]$ ,$c[i]$ 的直接后继为$c[i+lowbit(i)]$

前驱，即$c[i]$ 的直接前驱的直接前驱，即$c[i]$ 左侧所有子树的根

后继，即$c[i]$ 直接后继的直接后继，即$c[i]$ 的所有祖先

查询前缀和

$c[i]$ 的前缀和$sum[i]$ 等于$c[i]$ 加上$c[i]$ 的前驱

1
2
3
4
5
6
7
int sum(int i){
    int s = 0;
    for(;i>0;i-=lowbit(i)){
        s+=c[i];
    }
    return s;
}

点更新

若对$a[i]$ 修改，则只需要对$c[i]$ 及其所有的后继（祖先节点）进行修改即可，不需要修改其他节点

1
2
3
4
5
void add(int i,int v){
    for(;i<=n;i+=lowbit(i)){
        c[i]+=v;
    }
}

注意：树状数组的下标必须从1开始，而不能从0开始，因为lowbit(i)=0会出现死循环

查询区间和

用前缀和数组的思想

1
2
3
int sum(int i,int j){
    return sum(j)-sum(i-1);
}

1/30

快速幂算法

1
2
3
4
5
6
7
8
9
10
11
12
int PowerMod(int a, int b, int c)
{
    int ans = 1;
    a = a % c;
    while(b>0) {
        if(b % 2 = = 1)
        	ans = (ans * a) % c;
        b = b/2;
        a = (a * a) % c;
    }
    return ans;
}

矩阵快速幂

就是把整数的乘法换成矩阵的乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//矩阵乘法    
static int[][] Mul(int[][] a,int[][] b, int n, int mod){
        int[][] temp = new int[n][n];
        for(int i = 0;i<n;++i){
            for(int j = 0;j<n;++j){
                for(int k = 0;k<n;++k){
                    temp[i][j] += ((a[i][k]%mod)*(b[k][j]%mod))%mod;
                    temp[i][j] %= mod;
                }
            }
        }
        return temp;
    }
    static int[][] FastPow(int[][] a,int p,int mod){
        int n = a.length;
        //对于矩阵乘法来说，应该初始化为单位矩阵
        int[][] res = new int[n][n];
        for(int i = 0;i<n;++i){
            res[i][i] = 1;
        }
        while(p>0){
            if(p%2==1) res = Mul(res,a,n,mod);
            p = p>>1;
            a = Mul(a,a,n,mod);
        }
        return res;
    }

2/8

贝祖定理

如果$ax+by=z$ 成立，那么一定满足$z$ 是$x$ 和$y$ 的最大公约数的倍数，$a,b,x,y,z$ 都是整数。

若java中，lc提交时出现int与二进制数不能进行位运算的错误，则给运算整体加上括号。

2的幂

判断一个数是2的幂的条件

1
2
3
n&(n-1)==0;
或者
n&(-n) = n;

交换法实现全排列

　　原理：假设以字符串第0个位置（也就是第一个字符）为起点，分别与后面的每一个位置对应的字符进行交换。直到k等于字符串最后一个位置时，就会排列出新的组合。

数组所能开辟的最大空间

  • 函数内申请的变量，数组，是在栈（stack）中申请的一段连续的空间。栈的默认大小为2M或1M，开的比较小。

  • 全局变量，全局数组，静态数组（static）则是开在全局区（静态区）（static）。大小为2G，所以能够开的很大。(1.5-1.8G之间)

    1e7 ——1e9

  • 而malloc、new出的空间，则是开在堆（heap）的一段不连续的空间。理论上则是硬盘大小。

dfs中的两个函数

约束函数：能否得到可行解的约束

限界函数：能否得到最优解的约束

#include<bits/stdc++.h>

包含c++目前所有的头文件

2/10

dfs求解组合问题时，每一次递归是树枝上加深深度，而for循环是遍历这一个树层，注意去重的逻辑，是在同一树层中去重。组合总和2，不排序好像没办法写。

2/12

解数独，dfs返回值是boolean类型的原因

找到一个正确的答案就可以直接返回，而不用再回溯去搜索了，也就是不用搜索完全部的情况。

java中char与int相互转换

1
2
3
4
5
6
7
// '1' -> 1
char c9 = '1';
int num9 = c9 - '0';

// 1 -> '1'
int num10 = 1;
char c10 = (char)(num10 + '0');

在c++中若是想输入字符，一定要格外小心，输入数字之后再输入字符，就一定要记得getchar()，输入字符前一定要记得getchar()，输入字符后若想换行，也要记得getchar()

memset()

memset()函数非常好用

第一个参数是一个指针，第二个参数是要初始化填入的值，第三个参数是要初始化的大小

比如：

1
2
3
4
5
6
int row[9][10];
int col[9][10];
int grid[9][10];
memset(row,0,sizeof(row));
memset(col,0,sizeof(col));
memset(grid,0,sizeof(grid));

这就是表示把三个二维数组的初始值都填入0

输入二维字符数组的两种方式

方法一

1
2
3
4
5
6
char Map[5][5];
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        scanf("%s",Map[i]);
    }

方法二

1
2
3
4
5
6
char Map[5][5];
int main(){
    scanf("%d",&n);
    for(int i=0;i<n;i++){
        cin>>Map[i];
    }

cin 输入默认情况下是忽略 回车，空格，tab等空白符

注意方格图中xy和ij的对应关系，如下

1
2
int m = grid.size();
int n = grid[0].size();

此时，m表示有几行，对应y轴

n表示有几列，对应x轴

遍历的时候若i与m对应，j与n对应，则

1
2
3
int x = j + d[k][0];
int y = i + d[k][1];
dfs(y,x);

注意终止条件中i，j与m，n的对应关系，这个是最重要的，自己定义的xy怎么都可以。

2/16

记忆化容器的选择

但使用布尔数组作为记忆化容器往往无法区分「状态尚未计算」和「状态已经计算，并且结果为 false」两种情况。

因此我们需要转为使用 int[石子列表下标][跳跃步数]，默认值 0 代表状态尚未计算，−1 代表计算状态为 false，1 代表计算状态为 true。

存哈希表的技巧：可以把数组中的数值存为x，数组下标存为y，这样便于查找

记忆化容器可以使用哈希表

若哈希表中需要存储的辨识关键字有多个，则可以采用字符串形式。比如青蛙过河中，可以采用k+"-"+i 的string形式存储，y值存储搜索成功或失败（没有搜索到则不在哈希表中）

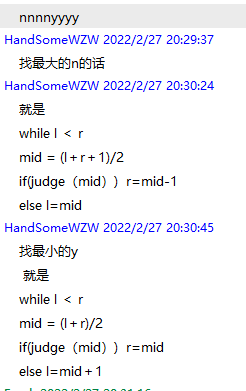
2/27

二分法查找符合条件的

1
2
3
4
5
6
7
8
9
10
11
12
13
while(l<r){
    //....
    if(check()){
    	l = mid + 1;
	}
	else{
    	r = mid;
	}
}


return r;
// return l;也对,因为此时l==r，才会退出循环

排序后，要找第一个符合条件的，这样分析

威哥讲解二分法

nnnyyy （n表示不满足条件，y表示满足条件）

满足条件了，就保持不变，即r = mid

不满足条件说明mid指向的是n，那么就l=mid＋1

找到一个符合条件的也不要急于返回，因为还可能有更优的，本题中对应，还有更小的符合条件的y

二分法的题目一定要注意取值范围，不行就把int变为long

位运算的优先级

非常低，运算时必须加括号，否则就会出错

111222333

找最小的2，就是（最左边的，符合条件的）

1
2
3
4
5
6
7
8
9
while(l<r){
    int mid = ((r-l)>>1)+l;
    if(nums[mid]<target){
        l = mid + 1;
    }else{
        r = mid;
    }
}
return r;

找最大的2，就是（最右边的，符合条件的）

1
2
3
4
5
6
7
8
9
while(l<r){
    int mid = ((r-l+1)>>1)+l;
    if(nums[mid]>target){
        r = mid - 1;
    }else{
        l = mid;
    }
}
return l;

符合条件，就保持不变，等于mid，而且if中的条件包含等于号的那一部分，也是等于mid，两者是相互对应的。(这个不适用全部的，还是要用check的思想来考虑问题)

找最左边的符合条件的，则r right遇到了就保持不变

找最右边的符合条件的，则l left遇到了就保持不变

二分法的本质

二分法的本质是二段性，并不是从一个有序数组中找出一个数（这只是二分法的一个应用）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
class Solution {
public:
    int search(vector<int>& nums, int target) {
        int n = nums.size();
        //通过二分找到分割点   整个数组中最小的元素
        if(n==0) return -1;
        if(n==1) return target==nums[0]?0:-1;
        int l = 0;
        int r = n-1;
        while(l<r){
            int mid = ((r-l+1)>>1)+l;
            if(nums[mid]>=nums[0]){
                l = mid;
            }else{
                r = mid - 1;
            }
        }
        if(target<nums[0]){
            //后半段二分
            l = l+1;
            r = n-1;
            while(l<r){
                int mid = ((r-l)>>1)+l;
                if(nums[mid]<target){
                    l = mid + 1;
                }else{
                    r = mid;
                }
            }
            return target==nums[r]?r:-1;
        }
        else{
            //前半段二分
            l = 0;
            while(l<r){
                int mid = ((r-l)>>1)+l;
                if(nums[mid]<target){
                    l = mid + 1;
                }else{
                    r = mid;
                }
            }
            return target==nums[r]?r:-1;
        }
    }
};

2/28

旋转数组

有序数组通过旋转转变为部分有序，要找出其中最小（最大）的元素，要使用二分法。

找到最大的元素比较方便，使用向上取整，l = mid，因为此时可以避免nums[mid]与nums[0]是同一个元素，避免了极端情况的错误。

找到最大元素的下标后，判断是不是最后一个元素，若是最后一个元素，则若找最小的元素要返回nums[0]；若不是最后一个元素，则返回nums[l+1]即可。

有重复元素的代码模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
class Solution {
public:
    int findMin(vector<int>& nums) {
        int n = nums.size();
        int l = 0;
        int r = n-1;
        while(r>0 && nums[0]==nums[r]) r--;
        if(r==l) return nums[l];
        while(l<r){
            int mid = ((r-l+1)>>1)+l;
            if(nums[mid]>=nums[0]) l = mid;
            else r = mid - 1;
        }
        if(l==n-1){
            return nums[0];
        }
        return nums[l+1];
    }
};

3/1

向上取整的方法

1
(n-1)/m+1;

3/7

快速将数字转成n进制表示的字符串

Integer.toString(int par1,int par2),par1表示要转成字符串的数字，par2表示要转成的进制表示，如：

Integer.toString(22,2),表示把22转成2进制表示的字符串，

Integer.toString(22,10),表示把22转成10进制表示的字符串，

Integer.toString(22,16),表示把22转成16进制表示的字符串，

Integer.toString(22,36),表示把22转成36进制表示的字符串，即10到36之间的数字表示为a到z的表示

二维前缀和模板

「二维前缀和」解决的是二维矩阵中的矩形区域求和问题。

二维前缀和数组中的每一个格子记录的是「以当前位置为区域的右下角（区域左上角恒定为原数组的左上角）的区域和」

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
// 预处理前缀和数组
{
    sum = new int[n + 1][m + 1];
    for (int i = 1; i <= n; i++) {
        for (int j = 1; j <= m; j++) {
            // 当前格子(和) = 上方的格子(和) + 左边的格子(和) - 左上角的格子(和) + 当前格子(值)【和是指对应的前缀和，值是指原数组中的值】
            sum[i][j] = sum[i - 1][j] + sum[i][j - 1] - sum[i - 1][j - 1] + matrix[i - 1][j - 1];
        }
    }
}

// 首先我们要令左上角为 (x1, y1) 右下角为 (x2, y2)
// 计算 (x1, y1, x2, y2) 的结果
{
    // 前缀和是从 1 开始，原数组是从 0 开始，上来先将原数组坐标全部 +1，转换为前缀和坐标
    x1++; y1++; x2++; y2++;
    // 记作 22 - 12 - 21 + 11，然后 不减，减第一位，减第二位，减两位
    // 也可以记作 22 - 12(x - 1) - 21(y - 1) + 11(x y 都 - 1)
    ans = sum[x2][y2] - sum[x1 - 1][y2] - sum[x2][y1 - 1] + sum[x1 - 1][y1 - 1];
}


前缀和、树状数组、线段树选择

针对不同的题目，我们有不同的方案可以选择（假设我们有一个数组）：

数组不变，求区间和：「前缀和」、「树状数组」、「线段树」

多次修改某个数，求区间和：「树状数组」、「线段树」

多次整体修改某个区间，求区间和：「线段树」、「树状数组」（看修改区间的数据范围）

多次将某个区间变成同一个数，求区间和：「线段树」、「树状数组」（看修改区间的数据范围）

这样看来，「线段树」能解决的问题是最多的，那我们是不是无论什么情况都写「线段树」呢？

答案并不是，而且恰好相反，只有在我们遇到第 4 类问题，不得不写「线段树」的时候，我们才考虑线段树。

因为「线段树」代码很长，而且常数很大，实际表现不算很好。我们只有在不得不用的时候才考虑「线段树」。

总结一下，我们应该按这样的优先级进行考虑：

简单求区间和，用「前缀和」
多次将某个区间变成同一个数，用「线段树」
其他情况，用「树状数组」

树状数组模板

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
// 上来先把三个方法写出来
{
    int[] tree;
    int lowbit(int x) {
        return x & -x;
    }
    // 查询前缀和的方法
    int query(int x) {
        int ans = 0;
        for (int i = x; i > 0; i -= lowbit(i)) ans += tree[i];
        return ans;
    }
    // 在树状数组 x 位置中增加值 u
    void add(int x, int u) {
        for (int i = x; i <= n; i += lowbit(i)) tree[i] += u;
    }
}

// 初始化「树状数组」，要默认数组是从 1 开始
{
    for (int i = 0; i < n; i++) add(i + 1, nums[i]);
}

// 使用「树状数组」：
{   
    void update(int i, int val) {
        // 原有的值是 nums[i]，要使得修改为 val，需要增加 val - nums[i]
        add(i + 1, val - nums[i]); 
        nums[i] = val;
    }
    
    int sumRange(int l, int r) {
        return query(r + 1) - query(l);
    }
}

求两个数组（一个数组也可以）中相加等于target的数对的个数

O(nlogn)

  1. 先对两个数组排序

  2. 用双指针法

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    //一个从头开始遍历，一个从尾开始遍历,和小于sum则左边++，和大于sum则右边--
    Arrays.sort(nums1);
    Arrays.sort(nums2);
    while(i<n && j>=0){
        if(nums1[i]+nums[j]<target){
            i++;
        }else if(nums1[i]+nums[j]>target){
            j--;
        }else{
            i++;
            j--;
            res++;
        }
    }

3/8

前缀和数组的下标数量通常比数组的下标数量多1.

树状数组需要结合差分数组才能完成区间修改+单点查询

差分数组

区间修改，单点查询

差分数组比原数组多一位，且最后一位什么也不表示，求前缀和的时候也不用管他。

可以看到，如果需要对LR 范围内所有数都进行相同的操作，我们不需要从LR遍历arr然后在每个值上进行相同操作，只需要在差分数组d中改变L和R+1的值即可。但是在查询arr数组中某个位置的数时，却要根据差分数组从前往后递推求值。（求前缀和）

3/10

连续异或运算也可以使用前缀异或，但是要利用一个特性：相同的值异或结果为0

本质上还是利用集合（区间结果）的容斥原理。只不过前缀和需要利用「减法（逆运算）」做容斥，而前缀异或是利用「相同数值进行异或结果为 00（偶数次的异或结果为 00）」的特性实现容斥.

归并排序求逆序对的数目

思想：每一次合并时，统计右边的数组对逆序对的贡献。若左边数组还没合并完成，右边的数先合并到总数组中，那么右边合并的数就会对逆序对产生贡献，产生的贡献为左边数组剩余的数字的数目

注意，归并排序中有一个优化，即在递归的过程中，若两个小数组分别排序后，合并之前，首先判断一下$nums[mid]$ 与$nums[mid+1]$ 的大小关系。若$$nums[mid] \leq nums[mid+1]$$

则可以直接返回左边数组的逆序对的数目+右边数组的逆序对的数目，而不必计算合并时产生的逆序对的数目$crossNum$ .但是注意，只有在合并函数merge中才有逆序对计数操作。

3/11

建图

建图，使用邻接表

1
2
3
4
5
6
7
8
9
10
11
List<Integer>[] children = new List[n];
        for(int i = 0;i<n;++i){
            children[i] = new ArrayList<>();
        }
        for(int i = 0;i<n;++i){
            if(parents[i]!=-1) 
            {
                children[parents[i]].add(i);
                // children[i].add(parents[i]);
            }
        }

建一个List数组，然后对每一个List元素，进行new ArrayList<>()

dfs返回以参数root为根的树的节点个数，但同时利用全局变量计算分数。若两次统计，会超时（先计算最大分数，再统计个数会超时）

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
int dfs(List<Integer>[] children,int n,int id){
        long score = 1;
        int sum = 1;
        for(int i = 0;i<children[id].size();++i){
            int t = dfs(children,n,children[id].get(i));
            sum += t;
            score *= t;
        }
        if(id!=0) score*=(n-sum);
        if(maxScore==score){
            count++;
        }else if(maxScore<score){
            maxScore = score;
            count=1;
        }
        return sum;
    }

那种深度优先遍历的题目，List里面嵌套List，记得res.add(path) 这样写是不对的，因为path后续修改时，也会修改res中的值，因为add的是引用。所以应当这样写：

1
res.add(new ArrayList<>(path));

3/12

注意

在写dfs的时候，要在一开始就写used[i]=true。一开始访问到就要把used数组置为true

使用dfs求连通分量的个数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int makeConnected(int n, int[][] connections) {
        //1.求边的条数m，m<n-1   -1
        //2.求连通分量的个数 mnum  然后-1
        if(connections.length<n-1) return -1;
        List<Integer>[] link = new List[n];
        for(int i = 0;i<n;++i){
            link[i] = new ArrayList<>();
        }
        for(int[] con:connections){
            link[con[0]].add(con[1]);
            link[con[1]].add(con[0]);
        }//建图完成
        boolean[] used = new boolean[n];
        int ans = 0;
        for(int i = 0;i<n;++i){
            if(!used[i]){
                dfs(i,used,link);
                ans++;
            }
        }
        return ans-1;
    }
    void dfs(int i,boolean[] used,List<Integer>[] link){
        used[i] = true;
        for(Integer j:link[i]){
            if(!used[j]){
                dfs(j,used,link);
            }
        }
    }

求最大连通分量

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
public int makeConnected(int n, int[][] connections) {
    //1.求边的条数m，m<n-1   -1
    if(connections.length<n-1) return -1;
    List<Integer>[] link = new List[n];
    for(int i = 0;i<n;++i){
        link[i] = new ArrayList<>();
    }
    for(int[] con:connections){
        link[con[0]].add(con[1]);
        link[con[1]].add(con[0]);
    }//建图完成
    boolean[] used = new boolean[n];
    int ans = 0;
    for(int i = 0;i<n;++i){
        if(!used[i]){
            ans = Math.max(dfs(i,used,link),ans);
        }
    }
    return ans;
}
int dfs(int i,boolean[] used,List<Integer>[] link){
    int t = 1;
    used[i] = true;
    for(Integer j:link[i]){
        if(!used[j]){
            t+=dfs(j,used,link);
        }
    }
    return t;
}

判断从start到target有没有通路，注意注意

dfs中不能直接返回

并查集

使用并查集统计有多少个连通分量：统计有多少个祖先 $fa[i]==i$

并查集实现注意点：为了避免出现二叉搜索树中的退化问题，要做到下面两点：

  1. 对于每棵树，记录这棵树的高度rank。
  2. 合并时如果两棵树的rank不同，则从rank小的向rank大的连边。

路径压缩

对于每个节点，一旦向上走到了一次根节点，就把这个点到父亲的边改为直接连向根。

在此之上，不仅仅是所查询的节点，在查询过程中向上经过的所有的节点，都改为直接连到根上。这样再次查询这些节点时，就可以很快知道是谁了。

在使用这种简化方法时，为了简单起见，即使树的高度发生了变化，我们也不修改rank的值。

并查集的实现

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
int par[MAX_N]; // 父亲
int rank[MAX_N]; // 树的高度
//初始化n个元素
void init(int n){
    for(int i = 0;i<n;++i){
        par[i] = i;
        rank[i] = 1;
    }
}
// 查询树的根
int find(int x){
    if(par[x]==x) return x;
    else return par[x]=find(par[x]);
}

// 合并x和y所属的集合
void unite(int x,int y){
    x = find(x);
    y = find(y);
    if(x==y) return;
    if(rank[x]<rank[y]){
        par[x] = y;
    }else{
        par[y] = x;
        if(rank[x]==rank[y]) rank[x]++;
    }
}

// 判断x和y是否属于同一个集合
bool same(int x,int y){
    return find(x)==find(y);
}

3/13

迪杰斯特拉算法 最短路

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
class Solution {
    public int networkDelayTime(int[][] times, int n, int k) {
        List<int[]>[] link = new List[n+1];
        for(int i = 1;i<=n;++i){
            link[i] = new ArrayList<>();
        }
        int[] dist = new int[n+1];
        Arrays.fill(dist,Integer.MAX_VALUE);
        for(int[] time:times){
            link[time[0]].add(new int[]{time[1],time[2]});
        }
        boolean[] used = new boolean[n+1];
        for(int i = 0;i<link[k].size();++i){
            dist[link[k].get(i)[0]] = link[k].get(i)[1];
        }
        used[k] = true;
        dist[0] = -1;
        dist[k] = 0;
        for(int i = 0;i<n-1;++i){//在S-V集合中进行n-1次搜索
            int temp = Integer.MAX_VALUE;
            int t = k;
            for(int j = 1;j<=n;++j)//寻找本轮循环中dist数组中的最小值
                if(!used[j] && dist[j]<temp){
                    temp = dist[j];//最小值是多少
                    t = j;//第几个节点
                }
            if(t==k) return -1;
            used[t] = true;
            for(int j = 0;j<link[t].size();++j){
                int to = link[t].get(j)[0];
                int w = link[t].get(j)[1];
                if(!used[to] && dist[to]>dist[t]+w){
                    dist[to] = dist[t]+w;
                }
            }
        }
        int res = Arrays.stream(dist).max().getAsInt();
        return res;
    }
}

堆优化的dijkstra

注意要有used数组来标识，否则会无限入堆，会超时

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
    private int[] Dijkstra(List<Integer>[] list,int n){
        boolean[] used = new boolean[n];
        int[] dist = new int[n];
        Arrays.fill(dist,INF);
        dist[0] = 0;
        Queue<int[]> que = new PriorityQueue<>((o1,o2)->o1[0]-o2[0]);
        que.offer(new int[]{dist[0],0});
        while(!que.isEmpty()){
            int[] info = que.poll();
            int from = info[1];
            int cost = info[0];
            if(used[from]) continue;
            used[from] = true;
            for(Integer l:list[from]){
                dist[l] = Math.min(dist[l],dist[from]+1);// 这里不推荐这样写 最好写cost+1，因为在求第二短的路径中这样写是错误的，而cost那样写就是对的
                que.offer(new int[]{dist[l],l});// 可以写一个if，只有更新时才入队，这样就可以不必使用used数组   
            }
        }
        return dist;
    }
		

// 创建一个数组存储最短路径上，每一个节点的前一个节点的编号。可利用此数组求出源点到任意一个节点的具体最短路径
// k是源点
        int[] p = new int[n+1];
        Arrays.fill(p,-1);
        for(int i = 0;i<list[k].size();++i){
            int[] info = list[k].get(i);
            p[info[0]] = k;
        }

// 下面就是求源点与某一个节点具体最短路径的步骤。注意k是源点，pre是终点
        int[] stack = new int[n+1];
        int top = 0;
        int pre = target;
        if(pre!=k) stack[top++]=pre;
        while(p[pre]!=-1 && p[pre]!=k){
            stack[top++] = p[pre];
            pre = p[pre];
        }
        stack[top++]=k;
        while(top>0){
            System.out.println(stack[--top]);
        }

3/18

存图方式

邻接矩阵

适用于边数较多的稠密图使用，当边数量接近点的数量的平方，即 m \approx n^2m≈n2 时，可定义为稠密图。

邻接表

链式前向星存图

适用于边数较少的稀疏图使用，当边数量接近点的数量，即 m \approx nm≈n 时，可定义为稀疏图。

类（边集数组）

Bellman-Ford算法使用，当然，该算法也可以使用邻接矩阵

0x3f3f3f3f

当作无穷大，很好用，无穷大加无穷大还是无穷大，并不会溢出

最后，0x3f3f3f3f还能给我们带来一个意想不到的额外好处：
如果我们想要将某个数组清零，我们通常会使用memset(a,0,sizeof(a))，方便又高效，但是当我们想将某个数组全部赋值为无穷大时，就不能使用memset函数而得自己写循环了，因为memset是按字节操作的，它能够对数组清零是因为0的每个字节都是0（一般我们只有赋值为-1和0的时候才使用它）。现在好了，如果我们将无穷大设为0x3f3f3f3f，那么奇迹就发生了，0x3f3f3f3f的每个字节都是0x3f！所以要把一段内存全部置为无穷大，我们只需要memset(a,0x3f,sizeof(a))。

3/19

链式前向星

有向图

img

无向图

img

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
public static void read(){
        n = s.nextInt();//节点数
        m = s.nextInt();//边数
        for (int i = 1; i <= m; i++) {//边的编号从1开始
            //head[node]是以node为起点的第一条边的编号
            //next[edge]是和edge同起点的下一条边的编号
            //to[edge]是编号为edge的这条边的终点
            //还可以加一个weighe[edge]表示边权
            int f = s.nextInt();
            int t = s.nextInt();
            next[2 * i] = head[f];
            to[2 * i] = t;
            head[f] = 2 * i;

            next[2 * i + 1] = head[t];
            to[2 * i + 1] = f;
            head[t] = 2 * i + 1;
        }
    }


 public static void read(){
        n = s.nextInt();//节点数
        m = s.nextInt();//边数
        for (int i = 1; i <= m; i++) {//边的编号从1开始
            //head[node]是以node为起点的第一条边的编号
            //next[edge]是和edge同起点的下一条边的编号
            //to[edge]是编号为edge的这条边的终点
            //还可以加一个weighe[edge]表示边权
            int f = s.nextInt();
            int t = s.nextInt();
            next[2 * i] = head[f];
            to[2 * i] = t;
            head[f] = 2 * i;

            next[2 * i + 1] = head[t];
            to[2 * i + 1] = f;
            head[t] = 2 * i + 1;
        }
        
        //用的话就是
        //for(int p = head[x]; p != 0; p = next[p]){
        //    dfs(to[p]);
        //}
    }

3/20

pair

因为pair重写了equals方法，往堆里放的话还要重写compareTo

https://gitee.com/dutsc/cloud-images/raw/master/images/202212041129879.png

这样写得到的是小顶堆

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
class E implements Comparable<E>{
    int x, y, z;
    public E(int a, int b, int c){
        x = a; y = b; z = c;
    }
    public int compareTo(E e){
        if(x < e.x) return 1;
        else if(x > e.x) return -1;
        else {
            if(y == e.y) return z - e.z;
            return y - e.y;
        }
    }
    public int hashCode(){
        return y*1000000 + z;
    }
    public int hashCode(){
        return Objects.hash(y,z);
    }

    public boolean equals(Object obj){
        if(obj == null){
            return false;
        }
        E e = (E)obj;
        if(this.y == e.y && this.z == e.z){
            return true;
        }else{
            return false;
        }
    }
    public String toString(){
        return "E("+x+","+y+","+z+")";
    }
}

学习一下Idea中hashCode的写法

扁平化

一般三个的数据可以把它变成两个，如a,b,w 坐标(a,b) 和权重w

结合数据范围，进行扁平化 把a,b变成1000*a+b这样的 也可以考虑变成字符串，然后再split

二维矩阵编号

二维矩阵中，将矩阵中的每一个单元格按顺序进行编号的方法：

这是一个通用的二维矩阵使用转为顺序编号的做法

记住对于 row * col 的矩阵，任意的点 (i,j) 可以使用 i * col + j 转化为顺序编码 idx （等价于从上往下 从左到右编号）

反过来将 idx 恢复成 (i,j) 表示只需要 (idx / col, idx % col) 即可

HashSet

放到HashMap key部分的元素，和放到HashSet部分的元素，需要同时重写hashCode()和equals()方法

3/22

dp与图论

只有拓扑图的图论问题，才能使用dp求解，若不是拓扑图，则只能使用图论的方法求解。

bfs超时问题

使用bfs时，注意used数组何时置为true很重要。

入队时把节点置为true 而不要出队时（也不一定）

dfs回溯问题

如果是纯粹的回溯问题，一定要确保每一步都要回溯，容易忘记回溯的几个地方

  1. sb.deleteCharAt(sb,length()-1);

  2. used[x] [y] = true
    …….

    used[x] [y] = false

如果是字符二维数组，则要确定是否访问过，并不需要多开一个used数组，直接把该位置的字符置成一个没有出现过的字符即可。

3/23

回溯时最容易忘记的部分

used数组是最容易忘记回溯的部分

矩阵快速幂

可以用于求解数列递推问题

矩阵快速幂用于求解一般性问题：给定大小为 n * n 的矩阵 M，求答案矩阵 M^k
，并对答案矩阵中的每位元素对 PP取模。

在上述两种解法中，当我们要求解 f[i] 时，需要将 f[0] 到 f[n−1] 都算一遍，因此需要线性的复杂度。

对于此类的「数列递推」问题，我们可以使用「矩阵快速幂」来进行加速（比如要递归一个长度为 1e9 的数列，线性复杂度会被卡）。

使用矩阵快速幂，我们只需要 O(\log{n}) 的复杂度。

矩阵乘法

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
const int N=100;
 
int c[N][N];
 
void multi(int a[][N],int b[][N],int n)//n是矩阵大小，n<N
 
{
 
memset(c,0,sizeof c);
 
for(int i=1;i<=n;i++)
 
for(int j=1;j<=n;j++)
 
for(int k=1;k<=n;k++)
 
c[i][j]+=a[i][k]*b[k][j];
 
}

字节常考

  1. K 个一组翻转链表

  2. 接雨水

  3. 合并K个排序链表

  4. 缺失的第一个正数 124. 二叉树中的最大路径和 76. 最小覆盖子串 32. 最长有效括号 72. 编辑距离 4. 寻找两个正序数组的中位数 239. 滑动窗口最大值 字节hard top10欢迎你

3/24

难以处理的边界问题

遇到难以处理的边界问题时，要灵活运用max(i-1,0) 和 min(i+1,m-1) 进行处理，而不是无谓地写很多if语句判断

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
class Solution {
    public int[][] imageSmoother(int[][] img) {
        int m = img.length;
        int n = img[0].length;
        int[][] temp = new int[m][n];
        for(int i = 0;i<m;++i){
            for(int j = 0;j<n;++j){
                int l = Math.max(i-1,0);
                int r = Math.min(m-1,i+1);
                int up = Math.max(j-1,0);
                int down = Math.min(j+1,n-1);
                int num = 0;
                int ans = 0;
                for(int x = l;x<=r;++x){
                    for(int y = up;y<=down;++y){
                        num++;
                        ans+=img[x][y];
                    }
                }
                temp[i][j] = ans/num;
            }
        }
        return temp;
    }
}

周赛那个k近邻也是一样

字典序

数字的字典序，就是根据数字的前缀进行排序

3/25

字符串去重

遇到字符串去重问题时，考虑统计以每一个字符结尾的长度最长的符合要求的字符串的数量，最后再加起来

3/30

乘积最大子数组

数据范围问题

https://gitee.com/dutsc/cloud-images/raw/master/images/202212041130517.png

注意这样的条件，若开静态数组，则要开10^6 范围的，因为可能会有99999的测试用例

4/1

若一个数组中的元素全都出现两次，只有一个元素出现一次，那么用异或运算即可求出单独的那一个.

1
2
3
4
5
int res = 0;
for(auto &x:nums){
    res^=x;
}
return res;

注意，这里使用&效率提升很大。

4/3

卡特兰数

$C_0 = 1$ $C_{n+1} = \frac{2(2n+1)}{n+2} C_n$

1
2
3
4
5
long long C = 1;
for(int i = 0;i<n;++i){
    C = C*2*(2*i+1)/(i+2);
}
return C;

例子1：凸n+2边形用其n-1条对角线把此凸n+2边形分割为互不重叠的三角形，有多少种方法？

例子2：圆周上共有2n个点，这2n个点配对可连成n条弦，且这些弦两两不相交的方式数有多少种？

例子3：在2n个顺序摆放的盒子中填充n个白球和n个黑球，要求任取前m个盒子，其中黑球数目不少于白球？

​ 变形：找钱问题：所有商品都是五角，但又n个人手里拿1块钱，n个人手里拿5角钱，如何给这n个人排序，使得不会出现找不开钱的情况（店家一开始钱为0）

https://gitee.com/dutsc/cloud-images/raw/master/images/202212041130362.png

例子4：给定n个实数x1,x2,…,xn的一个排列，在不改变数字顺序的前提下，只通过添加括号改变运算顺序，共有多少种方法？

https://gitee.com/dutsc/cloud-images/raw/master/images/202212041131287.png

4/5

线段树板子2

给区间内的每个数都乘以K，使用两个懒标记

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
//
// Created by s'c on 2022/4/5.
//
#include "iostream"
using namespace std;
typedef long long ll;
const int MAX = 1000010;
int mod;
ll nums[MAX];
struct node{
    int l;
    int r;
    ll add;
    ll mul;
    ll sum;
};
node tree[MAX<<2];

void pushup(int node){
    tree[node].sum = (tree[node<<1].sum + tree[node<<1|1].sum)%mod;
}

void build(int node, int L,int R){
    tree[node].l = L;
    tree[node].r = R;
    tree[node].mul = 1;
    tree[node].add = 0;
    if(L==R){
        tree[node].sum = nums[L]%mod;
        return;
    }
    int mid = ((R-L)>>1)+L;
    build(node<<1,L,mid);
    build(node<<1|1,mid+1,R);
    pushup(node);
}

void pushdown(int node){
    if(tree[node].mul!=1){
        tree[node<<1].mul = (tree[node<<1].mul * tree[node].mul)%mod;
        tree[node<<1|1].mul = (tree[node<<1|1].mul * tree[node].mul)%mod;
        tree[node<<1].add = (tree[node<<1].add * tree[node].mul)%mod;
        tree[node<<1|1].add = (tree[node<<1|1].add * tree[node].mul)%mod;
        tree[node<<1].sum = (tree[node<<1].sum * tree[node].mul)%mod;
        tree[node<<1|1].sum = (tree[node<<1|1].sum * tree[node].mul)%mod;
        tree[node].mul = 1;
    }
    if(tree[node].add){
        tree[node<<1].add = (tree[node<<1].add + tree[node].add)%mod;
        tree[node<<1].sum = (tree[node<<1].sum + tree[node].add*(tree[node<<1].r-tree[node<<1].l+1)%mod)%mod;
        tree[node<<1|1].add = (tree[node<<1|1].add + tree[node].add)%mod;
        tree[node<<1|1].sum = (tree[node<<1|1].sum + tree[node].add*(tree[node<<1|1].r-tree[node<<1|1].l+1)%mod)%mod;
        tree[node].add = 0;
    }
}

void update(int node,int L,int R,ll v1,ll v2){
    if(L<=tree[node].l && R>=tree[node].r){
        // v1产生的影响
        tree[node].mul = (tree[node].mul * v1)%mod;
        tree[node].add = (tree[node].add * v1)%mod;
        tree[node].sum = (tree[node].sum * v1)%mod;

        //v2产生的影响
        tree[node].add = (tree[node].add + v2)%mod;
        tree[node].sum = (tree[node].sum + v2*(tree[node].r-tree[node].l+1)%mod)%mod;
        return ;
    }
    int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
    pushdown(node);
    if(L<=mid) update(node<<1,L,R,v1,v2);
    if(R>mid) update(node<<1|1,L,R,v1,v2);
    pushup(node);
}

ll query(int node,int L,int R){
    if(R<tree[node].l || L>tree[node].r) return 0;
    if(L<=tree[node].l && R>=tree[node].r) return tree[node].sum;
    int mid = ((tree[node].r-tree[node].l)>>1)+tree[node].l;
    pushdown(node);
    ll res = 0;
    if(L<=mid) res = (res + query(node<<1,L,R))%mod;
    if(R>mid) res = (res + query(node<<1|1,L,R))%mod;
    return res;
}

int main(){
    int n,m,p;
    scanf("%d%d%d",&n,&m,&p);
    mod = p;
    for(int i = 0;i<n;++i){
        scanf("%ld",&nums[i]);
    }
    build(1,0,n-1);
    while(m-->0){
        int tt;
        scanf("%d",&tt);
        if(tt==1){
            // mul
            int x,y;
            ll k;
            scanf("%d%d%ld",&x,&y,&k);
            update(1,x-1,y-1,k,0);// 先乘后加
        }else if(tt==2){
            // add
            int x,y;
            ll k;
            scanf("%d%d%ld",&x,&y,&k);
            update(1,x-1,y-1,1,k);
        }else if(tt==3){
            // sum
            int x,y;
            scanf("%d%d",&x,&y);
            long t = query(1,x-1,y-1);
            printf("%ld\n",t);
        }
    }
}

注意

这个代码第一次写有两个地方出现错误

  1. tree[node].mul 要在build时进行初始化，不然编译器会自动初始化为0.这不是我们想要的。要手动初始化为1.
  2. 每一个步骤都要检查 node << 1 还是 node << 1|1，还是 node 想好了再去写，写完要检查一遍。
  3. 在build中对结构体数组中的变量进行初始化是一个好习惯。包括java中对对象数组的初始化，一定要进行。

埃氏筛法求质数

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
class Solution {
    public int countPrimes(int n) {
        int res = 0;
        int[] isSu = new int[n];
        Arrays.fill(isSu,1);
        for(int i = 2;i<n;++i){
            if(isSu[i]==1){
                res++;
                if((long)i*i<n){
                    for(int j = i*i;j<n;j+=i){
                        isSu[j] = 0;
                    }
                }
            }
        }
        return res;
    }
}

4/6

两次扫描与换根法

树形dp的应用

对于某种需要以每个节点为根进行一次DFS的题目，可以使用两次DFS扫描与换根法解决，实际上是利用递推式来一次求解的。

parseInt与valueOf的区别

  1. 返回值不同
    parseInt 返回值是int型
    valueof 返回值是Integer型

  2. valueof就是调用了parseInt方法的

  3. parseInt效率比valueof效率高

ACM模式的Java输入

1
2
3
4
5
6
7
8
9
10
11
12
13
import java.io.*;
import java.util.*;
public static Main{
    public statci void main(String[] args) throws IOException{
        BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
        String[] tt = br.readLine().split(" +");
        int n = tt.length;
        int[] ans = new int[n];
        for(int i = 0;i<n;++i){
            ans[i] = Integer.parseInt(tt[i]);
        }
    }
}

java输入二维数组，

记得抛出IOException异常

1
2
3
4
5
6
7
8
9
10
11
12
// java输入二维数组
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		int m = Integer.parseInt(br.readLine());
		int n = 0;
		for(int i = 0;i<m;++i) {
			String[] tt = br.readLine().split(" +");
			n = tt.length;
			for(int j = 0;j<n;++j) {
				ans[i][j] = Integer.parseInt(tt[j]);
			}
		}
		br.close();

java之ACM注意点

Java输入输出基本操作

Java之ACM注意点

\1. 类名称必须采用public class Main方式命名

\2. 在有多行数据输入的情况下，一般这样处理：

static Scanner in = new Scanner(System.in);

while(in.hasNextInt())

或者是

while(in.hasNext())

\3. 有关System.nanoTime()函数的使用，该函数用来返回最准确的可用系统计时器的当前值，以毫微秒为单位。

long startTime = System.nanoTime();

// … the code being measured …

long estimatedTime = System.nanoTime() - startTime;

Java之输入输出处理

输入

格式1：Scanner sc = new Scanner (new BufferedInputStream(System.in));

格式2：Scanner sc = new Scanner (System.in);

在读入数据量大的情况下，格式1的速度会快些。

读一个整数： int n = sc.nextInt(); 相当于 scanf(“%d”, &n); 或 cin >> n;

读一个字符串：String s = sc.next(); 相当于 scanf(“%s”, s); 或 cin >> s;

读一个浮点数：double t = sc.nextDouble(); 相当于 scanf(“%lf”, &t); 或 cin >> t;

读一整行： String s = sc.nextLine(); 相当于 gets(s); 或 cin.getline(…);

判断是否有下一个输入可以用sc.hasNext()或sc.hasNextInt()或sc.hasNextDouble()或sc.hasNextLine()

例1：读入整数

Input 输入数据有多组，每组占一行，由一个整数组成。

Sample Input

56

67

100

123

1
2
3
4
5
6
7
8
9
10
11
12
import java.util.Scanner;

public class Main {

public static void main(String[] args) {
    Scanner sc =new Scanner(System.in);
    while(sc.hasNext()){ //判断是否结束
    int score = sc.nextInt();//读入整数
    …………
   }
  }
}

例2：读入实数

输入数据有多组，每组占2行，第一行为一个整数N，指示第二行包含N个实数。

Sample Input

4

56.9 67.7 90.5 12.8

5

56.9 67.7 90.5 12.8

1
2
3
4
5
6
7
8
9
10
11
12
13
import java.util.Scanner;
public class Main {
public static void main(String[] args) {
    Scanner sc =new Scanner(System.in);
    while(sc.hasNext()){
      int n = sc.nextInt();
      for(int i=0;i<n;i++){
        double a = sc.nextDouble();
        ……………
      }
    }
  }
}

例3：读入字符串【杭电2017 字符串统计】

输入数据有多行，第一行是一个整数n，表示测试实例的个数，后面跟着n行，每行包括一个由字母和数字组成的字符串。

Sample Input

2

asdfasdf123123asdfasdf

asdf111111111asdfasdfasdf

import java.util.Scanner;

public class Main {

public static void main(String[] args) {

​ Scanner sc = new Scanner(System.in);

​ int n = sc.nextInt();

​ for(int i=0;i<n;i++){

​ String str = sc.next();

​ ……

​ }

}

}

import java.util.Scanner;

public class Main {

public static void main(String[] args) {

​ Scanner sc = new Scanner(System.in);

​ int n = Integer.parseInt(sc.nextLine());

​ for(int i=0;i<n;i++){

​ String str = sc.nextLine();

​ ……

​ }

}

}

输出

函数：

System.out.print();

System.out.println();

System.out.format();

System.out.printf();

例4 杭电1170Balloon Comes!

Give you an operator (+,-,*, / –denoting addition, subtraction, multiplication, division respectively) and two positive integers, your task is to output the result.

Input

Input contains multiple test cases. The first line of the input is a single integer T (0<T<1000) which is the number of test cases. T test cases follow. Each test case contains a char C (+,-,*, /) and two integers A and B(0<A,B<10000).Of course, we all know that A and B are operands and C is an operator.

Output

For each case, print the operation result. The result should be rounded to 2 decimal places If and only if it is not an integer.

Sample Input

4

+ 1 2

- 1 2

* 1 2

/ 1 2

Sample Output

3

-1

2

0.50

import java.util.Scanner;

public class Main {

public static void main(String[] args) {

​ Scanner sc =new Scanner(System.in);

​ int n = sc.nextInt();

​ for(int i=0;i<n;i++){

​ String op = sc.next();

​ int a = sc.nextInt();

​ int b = sc.nextInt();

​ if(op.charAt(0)==’+’){

​ System.out.println(a+b);

​ }else if(op.charAt(0)==’-‘){

​ System.out.println(a-b);

​ }else if(op.charAt(0)==’*’){

​ System.out.println(a*b);

​ }else if(op.charAt(0)==’/‘){

​ if(a % b == 0) System.out.println(a / b);

​ else System.out.format(“%.2f”, (a / (1.0*b))). Println();

​ }

​ }

}

}

格式化的输出

函数：

// 这里0指一位数字，#指除0以外的数字(如果是0，则不显示),四舍五入.

DecimalFormat fd = new DecimalFormat(“#.00#”);

DecimalFormat gd = new DecimalFormat(“0.000”);

System.out.println(“x =” + fd.format(x));

System.out.println(“x =” + gd.format(x));

public static void main(String[] args) {

NumberFormat formatter = new DecimalFormat( “000000”);

String s = formatter.format(-1234.567); // -001235

System.out.println(s);

formatter = new DecimalFormat( “##”);

s = formatter.format(-1234.567); // -1235

System.out.println(s);

s = formatter.format(0); // 0

System.out.println(s);

formatter = new DecimalFormat( “##00”);

s = formatter.format(0); // 00

System.out.println(s);

formatter = new DecimalFormat( “.00”);

s = formatter.format(-.567); // -.57

System.out.println(s);

formatter = new DecimalFormat( “0.00”);

s = formatter.format(-.567); // -0.57

System.out.println(s);

formatter = new DecimalFormat( “#.#”);

s = formatter.format(-1234.567); // -1234.6

System.out.println(s);

formatter = new DecimalFormat( “#.######”);

s = formatter.format(-1234.567); // -1234.567

System.out.println(s);

formatter = new DecimalFormat( “.######”);

s = formatter.format(-1234.567); // -1234.567

System.out.println(s);

formatter = new DecimalFormat( “#.000000”);

s = formatter.format(-1234.567); // -1234.567000

System.out.println(s);

formatter = new DecimalFormat( “#,###,###”);

s = formatter.format(-1234.567); // -1,235

System.out.println(s);

s = formatter.format(-1234567.890); // -1,234,568

System.out.println(s);

// The ; symbol is used to specify an alternate pattern for negative values

formatter = new DecimalFormat( “#;(#) “);

s = formatter.format(-1234.567); // (1235)

System.out.println(s);

// The ‘ symbol is used to quote literal symbols

formatter = new DecimalFormat( “ ‘# ‘# “);

s = formatter.format(-1234.567); // -#1235

System.out.println(s);

formatter = new DecimalFormat( “ ‘abc ‘# “);

s = formatter.format(-1234.567); // - abc 1235

System.out.println(s);

formatter = new DecimalFormat( “#.##%”);

s = formatter.format(-12.5678987);

System.out.println(s);

}

字符串处理String

String 类用来存储字符串，可以用charAt方法来取出其中某一字节，计数从0开始：

String a = “Hello”; // a.charAt(1) = ‘e’

用substring方法可得到子串，如上例

System.out.println(a.substring(0, 4)) // output “Hell”

注意第2个参数位置上的字符不包括进来。这样做使得 s.substring(a, b) 总是有 b-a个字符。

字符串连接可以直接用 + 号，如

String a = “Hello”;

String b = “world”;

System.out.println(a + “, “ + b + “!”); // output “Hello, world!”

如想直接将字符串中的某字节改变，可以使用另外的StringBuffer类。

高精度

BigInteger和BigDecimal可以说是acmer选择java的首要原因。

函数：add, subtract, divide, mod, compareTo等，其中加减乘除模都要求是BigInteger(BigDecimal)和BigInteger(BigDecimal)之间的运算，所以需要把int(double)类型转换为BigInteger(BigDecimal)，用函数BigInteger.valueOf().

import java.io.BufferedInputStream;

import java.math.BigInteger;

import java.util.Scanner;

public class Main {

public static void main(String[] args) {

Scanner cin = new Scanner (new BufferedInputStream(System.in));

int a = 123, b = 456, c = 7890;

BigInteger x, y, z, ans;

x = BigInteger.valueOf(a);

y = BigInteger.valueOf(b);

z = BigInteger.valueOf(c);

ans = x.add(y); System.out.println(ans);

ans = z.divide(y); System.out.println(ans);

ans = x.mod(z); System.out.println(ans);

if (ans.compareTo(x) == 0) System.out.println(“1”);

}

}

进制转化

String st = Integer.toString(num, base); // 把num当做10进制的数转成base进制的st(base <= 35).

int num = Integer.parseInt(st, base); // 把st当做base进制，转成10进制的int(parseInt有两个参数,第一个为要转的字符串,第二个为说明是什么进制).

BigInter m = new BigInteger(st, base); // st是字符串，base是st的进制.

进制转换

使用Integer.toString(ta,base)函数将int类型的ta转换成base进制的String

1
2
3
4
5
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String tt = br.readLine();
int a = Integer.parseInt(tt);
String ta = Integer.toString(a,2);
System.out.println(ta);

使用Integer.parseInt(ta,base) 将String类型，base进制的ta转换成10进制的int

1
2
3
4
BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
String tt = br.readLine();
int a = Integer.parseInt(tt,2);
System.out.println(a);

4/7

求一个数的所有不重复的因子

1
2
3
4
5
6
7
8
9
10
11
12
13
14
Scanner sc = new Scanner(System.in);
int n = sc.nextInt();
List<Integer> list = new ArrayList<>();
Set<Integer> set = new LinkedHashSet<>();
double sq = Math.sqrt(n);
for(int i = 1;i<=sq;++i){
    if(n%i==0){
        set.add(i);
        set.add(n/i);
    }
}
for(Integer i:set){
    System.out.print(i+" ");
}

4/8

多数去重的思路

多个数字组成的整体（如int[2]，最简分数去重等等），常规的去重思路

找一个基数，这个基数比最大的数据范围还要大，使用如下形式将其放入数组中存储（若数据量大就放入哈希表存储）

1
2
3
4
5
// 假设a，b数据的最大范围是[0-25]
int getIndex(int a,int b){
    return 30*a+b;
}
int[] ans = new int[30*30+30];

这样，只要a不变，任凭b怎么变化，getIndex得到的值都会不一样，就达到了去重的目的。

同理，若是有abc三个数，则去重的基数就要再加一个

1
2
3
4
int getIndex(int a,int b,int c){
    return 30 * 30 * a + 30 * b + c;
}
int[] ans = new int[30*30*30+30*30+30];

4/11

查找相邻元素

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
adjacent_find(iterator beg, iterator end);
// 查找相邻重复元素,返回相邻元素的第一个位置的迭代器
    vector<int> a;
    a.emplace_back(1);
    a.emplace_back(5);
    a.emplace_back(6);
    a.emplace_back(2);
    a.emplace_back(9);
    a.emplace_back(3);
    vector<int>::iterator it = adjacent_find(a.begin(),a.end());
    if(it!=a.end()){
        cout << "找到了" << endl;
    }else {
        cout << "没找到" << endl;
    }
    cout << *it << endl;

4/12

寻找第k个缺失的数

找到一个严格升序排列的正整数组中第k个缺失的正整数。

我们发现截至到每一个位置，缺失的正整数的数量 是非递减的，于是可以考虑使用二分法，但要注意边界情况的处理。

二分法找某一个值

使用二分法找某一个符合条件的值时，要先求，然后再验证是否符合条件。因为求的是yyynnn 或者 nnnyyy类型的，可能边界值不符合题目条件。

c++字符串越界

越界之后不会报错，而是取到一个’/0’字符

1
2
3
4
5
6
7
    string s = "123";
    cout << (int)s[6] << endl;
    int a = ' ';
    cout <<  a << endl;
    return 0;
//0  
// 32

拆分正整数为几个数的和，使其乘积最大

1
2
3
4
5
if(n<=3) return n-1;
int x = n/3,y = n%3;
if(y==0) return pow(3,x);
if(y==1) return pow(3,x-1)*4;
return pow(3,x)*2;

4/13

线段树暴力求解

线段树中的暴力问题，如对$a_i$ 连续取模，可以在$loga_i$复杂度之内实现，故可以暴力求解

$x % p < \frac{x}{2}$ $p<x$

第一次写，问题：

  1. build中当l==r 时没有写return ;
  2. 区间暴力取模，要到了单点的时候再取模，即tr[node].r==tr[node].l时
  3. 所有update modify的最后一步一定是pushup，而不是return。一定要向上回溯
  4. update单点更新到叶子节点时，不论该节点的lr是不是k，都要return了，注意要把return写在k if的外面。

4/14

欧拉函数就是指:给定一个n，求得1到n中与n互质的数的个数

1.如果n,m互质，那么 : φ(n*m) = φ(n)*φ(m)

2.如果n为质数，那么 : φ(n) = n-1，可推出1中φ(n * m) = (n-1)*(m-1)

3.如果n % m == 0，那么 : φ(n * m) = m * φ(n)

4.在3的基础上 : if(n % m == 0 && φ(n / m)%m == 0) φ(n) = φ(n/m)*m

5.在3的基础上 : if(n % m == 0 && φ(n / m)%m != 0) φ(n) = φ(n/m)*(m-1)

6.当n为奇数时，φ(n) = φ(2*n)

7.与小于等于n中，与n互质的数之和为:φ(n)*n/2

dfs

问题

给定一个序列，一个数k，问是否能从序列中找到若干个数，使得其和为k，序列中的数只能使用一次

https://www.papamelon.com/problem/201

分析

本题是一个子集树问题（选或不选2^n），与之类似的还有排列树问题（每次少一个，n!），n叉树问题（n^n），代码结构如下：

1
2
3
4
5
6
7
8
9
10
11
12
dfs(int i){
  //1 输出结果
  if(i==n) printf();
  
  //2 剪枝
  
  //3 遍历下一层
  for(int j = 0;j<k;++j){ // 子集树
  for(int j = i;j<=n;++j{ // 排列树
  for(int j = 0;j<n;++j{  // n叉树
    dfs(i+1);
}

第一份超时代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
// 超时
#include "iostream"
using namespace std;
typedef  long long ll;
ll arr[21]={0};
bool used[21]={0};
bool dfs(ll* arr,int k,int now,int n){
    if(now==k) return true;
    for(int i = 1;i<=n;++i){
        if(!used[i]){
            used[i] = true;
            if(dfs(arr,k,now+arr[i],n)) return true;
            used[i] = false;
        }
    }
    return false;
}
int main(){
    int n;
    while(scanf("%d",&n)!=EOF){
        for(int i = 1;i<=n;++i){
            scanf("%lld",&arr[i]);
        }
        ll k;
        scanf("%lld",&k);
        for(int i = 0;i<21;++i){
            used[i] = 0;
        }
        if(dfs(arr,k,0,n)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

很容易写出本题代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
#include "iostream"
using namespace std;
typedef long long ll;
ll a[21]={0};
int n;
ll k;
bool dfs(int i,int sum){
    if(i==n) return sum==k;
    if(dfs(i+1,sum)){
        printf("没取%lld ",a[i]);
        return true;
    }
    if(dfs(i+1,sum+a[i])){
        printf("取了%lld ",a[i]);
        return true;
    }
    return false;
}
int main(){
    while(scanf("%d",&n)!=EOF){
        for(int i = 0;i<n;++i){
            scanf("%lld",&a[i]);
        }
        scanf("%lld",&k);
        if(dfs(0,0)) printf("Yes\n");
        else printf("No\n");
    }
    return 0;
}

这里我也给出输出全排列的代码：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
#include "iostream"
#include "vector"
using namespace std;
vector<int> b;
int id = 0;
void dfs(vector<int>& arr,int i,int n,vector<bool>& used){
    if(i==n){
        for(int j = 0;j<n;++j){
            cout << b[j] << " ";
        }
        id++;
        cout << endl;
    }
    for(int j = 0;j<n;++j){
        if(!used[j]){
            used[j] = true;
            b.emplace_back(arr[j]);
            dfs(arr,i+1,n,used);
            b.pop_back();
            used[j] = false;
        }
    }
}
int main(){
    vector<int> arr(6,0);
    int n = arr.size();
    for(int i = 0;i<n;++i){
        arr[i] = i+1;
    }
    vector<bool> used(n,0);
    dfs(arr,0,n,used);
    cout << "id=" << id << endl;
    return 0;
}

贪心

n项工作，每项工作si开始，ti结束，每次只能同时参与一项工作，问最多参与多少个工作？

结论

在可选的工作中，每次都选取结束时间最早的工作，可以实现参与最多的工作。、

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
//
// Created by s'c on 2022/4/14.
//
#include "iostream"
#include "algorithm"
using namespace std;
const int MAX = 100010;
typedef long long ll;
ll s[MAX];
ll t[MAX];

int n;

int main(){
    pair<ll,ll> pp[MAX];
    while(scanf("%d",&n)!=EOF){
        for(int i = 0;i<n;++i){
            scanf("%lld",&s[i]);
            scanf("%lld",&t[i]);
            pp[i].first = t[i];
            pp[i].second = s[i];
        }
        sort(pp,pp+n);
        int res = 0;
        ll last = 0;
        for(int i = 0;i<n;++i){
            if(last<pp[i].second){
                res++;
                last = pp[i].first;
            }
        }
        printf("%d\n",res);
    }
}

priority_queue的pair自定义排序

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
struct cmp{
        template<typename T, typename U>
        bool operator()(T const& left, U const &right) {
            if (left.second < right.second) return true;
            return false;
        }
    };
...
int main(){
    unordered_map<int, int> mp;
    mp[3]=4;
    mp[2]=44;
    mp[12]=432;
    priority_queue<pair<int, int>, vector<pair<int, int>>, cmp>  pq(mp.begin(), mp.end());//完成pq的初始化
}

cmp中，>表示降序

另外几种常用的

1
2
3
4
5
priority_queue< int > q;// 默认是 从大到小。 
priority_queue < int , vector<int> ,less<int> > q;//从大到小 
priority_queue < int , vector<int>, greater<int> > q; //从小到大，需要vector
priority_queue < int , vector<int> , cmp1  > q;//从大到小，需要vector
priority_queue < int , vector<int> , cmp  > q;//从小到大，需要vector

离散化

1 2 5000 900000

变成 0 1 2 3

只表示相对大小，而不用来表示数值大小

函数lower_bound()在first和last中的前闭后开区间进行二分查找，返回大于或等于val的第一个元素位置。如果所有元素都小于val，则返回last的位置

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
//
// Created by s'c on 2022/4/13.
//
#include "iostream"
#include "cstring"
#include "algorithm"
using namespace std;
int A[10010]={0};
int B[10010]={0};
int f[2][10010]={0};
const int INF = 0x3f3f3f3f;
int main() {
    int n = 6;
    int a[]={0,1,2,900,50000,6000000,90000000};
    int te[7] = {0};
    int ls[7] = {0};
    for(int i=1;i<=n;i++){
        scanf("%d",&a[i]);
        te[i]=a[i];
    }
    sort(te+1,te+n+1);
    int size=unique(te+1,te+n+1)-te-1;
    for(int i=1;i<=n;i++){
        ls[i]=lower_bound(te+1,te+size+1,a[i])-te-1;
        cout << ls[i] << " ";
    }
}

包含unique函数的用法

使用之前必须先排序，unique返回一个迭代器，它指向不重复的最后一个数据的下标。

一般不常用，只在离散化中用到，但是离散化也可以用哈希表代替。

c++中的unordered_map

unordered_map的用法和map是一样的，提供了 insert，size，count等操作，并且里面的元素也是以pair类型来存贮的。其底层实现是完全不同的，但是就外部使用来说却是一致的。

使用

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
//
// Created by s'c on 2022/4/15.
//
#include "iostream"
#include "map"
#include "unordered_map"
#include "string"
using namespace std;

int main(){
    unordered_map<int, string> myMap={{ 5, "张大" },{ 6, "李五" }};//使用{}赋值
    myMap[2] = "李四";  //使用[ ]进行单个插入，若已存在键值2，则赋值修改，若无则插入。
    myMap.insert(pair<int, string>(3, "陈二"));//使用insert和pair插入
    //遍历输出+迭代器的使用
    auto iter = myMap.begin();//auto自动识别为迭代器类型unordered_map<int,string>::iterator
    while (iter!= myMap.end())
    {
        cout << iter->first << "," << iter->second << endl;
        ++iter;
    }

    //查找元素并输出+迭代器的使用
    auto iterator = myMap.find(2);//find()返回一个指向2的迭代器
    if (iterator != myMap.end())
        cout << endl<< iterator->first << "," << iterator->second << endl;
    return 0;
}

注意：

  1. myMap[2]=”李四” 若没有pair<2,”李四”> ，则直接插入；若key 2已经存在，则修改key 2对应的value为”李四”。

  2. myMap.insert(make_pair(2,”王五”))，若myMap中没有pair<int,string>(2,”王五”)，则直接插入；若已经存在，则不再插入，也就是不修改，直接丢弃。

  3. pair的构造函数
    pair<int,string>(1,”李四”)
    make_pair(1,”李四”)

  4. 在使用unordered_map统计字符、数字出现频率时，可直接使用++myMap[i]; 若出现频率减为0，则要手动删除这个pair，即 myMap.erase(key)

    1
    2
    3
    if(myMap[i]==0){
        myMap.erase(i);
    }

遍历unordered_map的方法

需要使用迭代器

不是key和value，也不是.first 和.second 而是iter->first 和 iter->second

1
2
3
4
5
6
auto iter = myMap.begin();//auto自动识别为迭代器类型unordered_map<int,string>::iterator
while (iter!= myMap.end())
{
    cout << iter->first << "," << iter->second << endl;
    ++iter;
}

查找某一个元素并输出

不要使用这种方式！！！！！！！！！！！

1
cout << myMap[2] << endl;

因为这样如果unordered_map中不存在key 2的话，就会手动插入一个空的字符串，会改变原来的map的

而如果是<int,int> 则会插入默认value0

1
2
unordered_map<int,int> map;
cout << map[0] << endl;// 0

推荐使用迭代器

1
2
3
4
//查找元素并输出+迭代器的使用
auto iterator = myMap.find(2);//find()返回一个指向2的迭代器
if (iterator != myMap.end())
    cout << endl<< iterator->first << "," << iterator->second << endl;

4/17

尾随0的个数

重要结论：乘积尾随0的数量是所有乘数中因子2数量之和与因子5数量之和中的较小值。

在做乘法的过程中，尾随0的数量只会增加不会减少，因此我们应该让尽量多的数参与乘积运算。也就是说最优路径一定是从某个边界出发，拐个弯，再走到另一个边界，不会中途不走了或者不拐弯（这样参与运算的数不是尽量多的）。

因此先用前缀和维护每一行和每一列因子 2 与因子 5 的数量，再枚举拐点计算答案即可。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
class Solution {
public:
    int maxTrailingZeros(vector<vector<int>>& grid) {
        int n = grid.size(), m = grid[0].size();
        vector<vector<int>> f2(n + 1), g2(n + 1), f5(n + 1), g5(n + 1);
        for (int i = 0; i <= n; i++) f2[i] = g2[i] = f5[i] = g5[i] = vector<int>(m + 1);
        for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
            int x = grid[i - 1][j - 1];
            int two = 0, five = 0;
            while (x % 2 == 0) two++, x /= 2;
            while (x % 5 == 0) five++, x /= 5;
            f2[i][j] = f2[i][j - 1] + two;
            g2[i][j] = g2[i - 1][j] + two;
            f5[i][j] = f5[i][j - 1] + five;
            g5[i][j] = g5[i - 1][j] + five;
        }
        int ans = 0;
        for (int i = 1; i <= n; i++) for (int j = 1; j <= m; j++) {
            // 从左边出发，到上边结束
            ans = max(ans, min(f2[i][j] + g2[i - 1][j], f5[i][j] + g5[i - 1][j]));
            // 从左边出发，到下边结束
            ans = max(ans, min(f2[i][j] + g2[n][j] - g2[i][j], f5[i][j] + g5[n][j] - g5[i][j]));
            // 从右边出发，到上边结束
            ans = max(ans, min(f2[i][m] - f2[i][j] + g2[i][j], f5[i][m] - f5[i][j] + g5[i][j]));
            // 从右边出发，到下边结束
            ans = max(ans, min(f2[i][m] - f2[i][j] + g2[n][j] - g2[i - 1][j], f5[i][m] - f5[i][j] + g5[n][j] - g5[i - 1][j]));
        }
        return ans;
    }
};

4/19

给一个字符串s和一个字符c，返回一个和字符串等长的数组，其中每一个数都表示该数与最近的字符c之间的距离。

问题可以转换成，对 s 的每个下标 i，求

s[i] 到其左侧最近的字符 c 的距离
s[i] 到其右侧最近的字符 c 的距离
这两者的最小值。

4/24

求一个点被几个区间覆盖

差分+离散化+排序

转化为区间修改，单点查询的题目，使用差分来解决；由于数据量很大，使用哈希表离散化。

对per进行排序，相当于一个预处理，这样就可以让时间复杂度从n^2降低到nlogn

灵佬 灵神代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
class Solution {
public:
    vector<int> fullBloomFlowers(vector<vector<int>>& f, vector<int>& per) {
        map<int,int> m;
        int n = per.size();
        vector<int> res(n,0);
        for(auto& ff:f){
            int start = ff[0],end = ff[1];
            m[start]++;
            m[end+1]--;
        } 
        // 对person的下标按照person值进行排序
        vector<int> id(n);
        iota(id.begin(),id.end(),0);
        sort(id.begin(),id.end(),[&](int i,int j){return per[i]<per[j];});
        map<int,int>::iterator it = m.begin();
        int sum = 0;
        for(int i:id){
            int t = per[i];
            for(;it!=m.end() && it->first<=t;++it){
                sum+=it->second;
            }
            res[i] = sum;
        }
        return res;
    }
};

注意骚操作：对person数组按照值进行排序，并返回排好序的person数组的下标，这些下标对应的值已经按照person的值排好序。

1
2
3
vector<int> id(n);
iota(id.begin(), id.end(), 0);
sort(id.begin(), id.end(), [&](int i, int j) { return persons[i] < persons[j]; });

sort排序的原理

原理是 cmp返回值为真时，第一个数字放前面

1
2
3
bool cmp(int &a,int &b){
    return a>b;
}

lambda表达式

1
[ 捕获 ] ( 形参 ) -> ret { 函数体 };

lambda表达式一般都是以方括号[]开头，有参数就使用()，无参就直接省略()即可，最后结束于{}，其中的ret表示返回类型。

1
2
3
4
5
6
7
#include <iostream>
int main()
{
    auto atLambda = [] {std::cout << "hello world" << std::endl;};
    atLambda();
    return 0;
}

上面定义了一个最简单的lambda表达式，没有参数。如果需要参数，那么就要像函数那样，放在圆括号里面，如果有返回值，返回类型则要放在->后面，也就是尾随返回类型，当然你也可以忽略返回类型，lambda会帮你自动推导出返回类型，下面看一个较为复杂的例子：

assign()成员函数

优于for循环，好得多

区间成员函数优于与之对应的单元素成员函数。

erase()和insert()区间插入

1
2
3
4
5
6
7
8
9
10
11
int main(){
    vector<int> a(1,0);
    vector<int> b{1,2,3,4,5};
    a.assign(b.begin(),b.end());//1 2 3 4 5
//    a.insert(a.end(),b.begin(),b.end());//0 1 2 3 4 5
//    a.insert(a.begin(),b.begin(),b.end());// 1 2 3 4 5 0
    a.erase(a.begin(),a.begin()+2);//3 4 5
    for(int i = 0;i<a.size();++i){
        cout << a[i] << " ";
    }
}

4/25

a是已经排好序的序列，利用二分查找找出a中$a_i\leq k$ 的$a_i$ 的最小指针

1
lower_bound(a,a+n,k);

利用二分查找找出a中满足$a_i > k$ 的$a_i$ 的最小指针

1
upper_bound(a,a+n,k);

于是，我们可以求出，在有序序列a中k的个数

1
upper_bound(a,a+n,k)-lower_bound(a,a+n,k);

求划分数

n个无区别的物品，将他们划分成不超过m组，求有多少种划分方法（对M取模）

这样想，考虑n的m划分$a_i(\sum_{i=1}^m a_i=n)$ 如果对于每个$i$ 都有$a_i>0$ ，则$a_{i}-1$ 就对应了n-m的n划分。另外，如果存在$a_i=0$，那么就对应了n的m-1划分。综上可以得出递推关系如下所示。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
//
// Created by s'c on 2022/4/25.
//
#include "bits/stdc++.h"
using namespace std;
int n,m,M;
const int MAX = 1010;
int dp[MAX][MAX];//dp[i][j]表示j的i划分，把j划分成i份，有多少种划分方法

int main(){
    scanf("%d%d%d",&n,&m,&M);
    dp[0][0] = 1;
    for(int i = 1;i<=m;++i){
        for(int j = 0;j<=n;++j){
            if(j<i) dp[i][j] = dp[i-1][j];
            else dp[i][j] = (dp[i-1][j] + dp[i][j-i])%M;
        }
    }
    printf("%d\n",dp[m][n]);
}

若223 232 不算一组，则可以这样想 将j划分成i个，可以先取出k个，然后将剩下的j-k个分成i-1份，递推式如下

$dp[i][j] = \sum_{k=0}^j dp[i-1][j-k]$

4/28

题目连接

https://www.papamelon.com/problem/225

思路

用dp[i][j]表示从前i中物品中取出j个，一共有多少种取法
dp[i][j]: 考虑前 i 种物品中选出 j 个物品的方案数
将物品的种类从 1∼n 编号，答案则是：dp[n][m]

根据状态定义我们发现，每种物品可能取1，2，…a_i种可能。
接下来进行分类讨论：

  1. 当$j<=a_i$时，$dp[i][j] = dp[i-1][j]+dp[i-1][j-1]+…+dp[i-1][1]+dp[i-1][0]$
  2. 当$j>a_i$时，$dp[i][j] = dp[i-1][j]+dp[i-1][j-1]+…+dp[i-1][j-a_i]$

设$b = min(ai,j)$，则
$dp[i][j] = dp[i-1][j]+dp[i-1][j-1]+…dp[i-1][j-b]$

但此时时间复杂度过高，每次求dp[i][j]都要遍历ai，这样复杂度为n*m*ai，一定会超时。考虑使用动态规划的递推思想优化。

优化

如何利用动态规划的递推思想呢？考虑对于$dp[i][j]$，若我们已知$dp[i][j-1]，$即$dp[i][j-1] = dp[i-1][j-1]+dp[i-1][j-2]+…+dp[i-1][j-1-b]，b = min(j-1,ai)$
此时还是要根据$j-1$与$a_i$的大小情况进行分类讨论

  1. $j-1<=a_i$时，$dp[i][j-1] = dp[i-1][j-1]+dp[i-1][j-2]+…+dp[i-1][0]$，有$dp[i][j] = dp[i][j-1]+dp[i-1][j]$

  2. $j-1>a_i$时，$dp[i][j-1] = dp[i-1][j-1]+dp[i-1][j-2]+…+dp[i-1][j-ai]+dp[i-1][j-1-a_i]$，有$dp[i][j] = dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1-a_i]$

    于是就得出了递推公式。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
//
// Created by s'c on 2022/4/28.
//
#include "bits/stdc++.h"
using namespace std;
const int MAX = 1010;	q` 
int dp[MAX][MAX]={0};
int a[MAX]={0};
int M=0;
int n,m;
void tt(){
    cin>>n>>m>>M;
    for(int i = 1;i<=n;++i){
        cin>>a[i];
    }
    for(int i = 0;i<=n;++i){
        dp[i][0] = 1;
    }
    for(int i = 1;i<=n;++i){
        for(int j = 1;j<=m;++j){
            if(j-1<a[i]){
                dp[i][j] = (dp[i][j-1]+dp[i-1][j])%M;
            }else{
                dp[i][j] = (dp[i][j-1]+dp[i-1][j]-dp[i-1][j-1-a[i]]+M)%M;
            }
        }
    }
    for(int i = 1;i<=n;++i){
        for(int j = 1;j<=m;++j){
            cout << dp[i][j] << " ";
        }
        cout << endl;
    }
    printf("%d\n",dp[n][m]);
}
int main(){
    tt();
    return 0;
}

注意

  1. 第一次写时，ai与dp[i][j]的对应关系没找好，注意ai是从0开始还是从1开始，dp[i][j]也要做相应的变化

题目连接226远征

https://www.papamelon.com/problem/226

思路讲解

本题也可采用贪心的思想去求解，只是为了求解方便，使用了优先队列数据结构。每次到加油站时，都要把加油站的油加光，这是贪心1；
另外，汽车不会加油，除非邮箱内的油不能支撑汽车到下一个加油站，这是贪心2.

另外，我们可以使用小技巧：每到一个加油站时，我们都默认获得了加油的资格，只是不把油加上，而是放到一个优先队列中（大顶堆）。
当需要加油的时候，就默认从优先队列中取出最大的，意思是在我到那个加油站的时候，已经加过油了。

失败条件：若当前邮箱里的油不能支撑汽车到下一个加油站了，但是优先队列已经空了，那么汽车不能到达终点，输出-1.

还有坑：

  1. 第一遍做时，没有注意到给出的Ai是该加油站到终点的距离。
  2. 给出的加油站的距离可能没有排好序，需要重新排序。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
//
// Created by s'c on 2022/4/28.
//
#include "bits/stdc++.h"
using namespace std;
int N,L,P;
const int MAX = 20010;

void solve(){
    vector<pair<int,int>> a;
    scanf("%d",&N);
    for(int i = 0;i<N;++i){
        int t1,t2;
        scanf("%d%d",&t1,&t2);
        a.emplace_back(t1,t2);
    }
    scanf("%d%d",&L,&P);
    int res = 0,pos = 0,tank = P;
//    a[N] = L;
//    b[N] = 0;
    a.emplace_back(0,0);
    sort(a.begin(),a.end(),[&](pair<int,int>& a,pair<int,int>& b)->bool {return a.first>b.first;});
//    for(int i = 0;i<=N;++i){
//        cout << "loc=" << a[i].first << " " << "you=" << a[i].second << endl;
//    }
    priority_queue<int> maxHeap;
    for(int i = 0;i<=N;++i){
        int loc = a[i].first;
        int ll = a[i].second;
        int d = L-loc-pos;
        while(tank<d){
            if(maxHeap.empty()){
                printf("-1\n");
                return;
            }
            int add = maxHeap.top();
            maxHeap.pop();
            tank+=add;
            res++;//加了一次油
        }
        pos = L-loc;
        tank-=d;
        maxHeap.push(ll);
    }
    printf("%d\n",res);
}
int main(){
    solve();
    return 0;
}

set查找集合中元素的方法

1
2
3
4
5
6
//方法一：使用迭代器
set<int>::iterator it = set.begin();
for(;it!=set.end();++it);

//方法二 使用count方法
set.count(2)>0  表明set中有元素2

set是有序哈希表，相当于TreeSet，不能存放重复元素。

map删除元素

1
2
map<int,int> m;
m.erase(key);

能存放重复值的multiset，重复键值的multimap

multiset还是有序的，multimap也还是有序的

5/1

快速排序不稳定，想要稳定，就要用下面的代码

1
2
3
4
// ca数组已经给出
vector<int> id(n);
iota(id.begin(),id.end(),0);
sort(id.begin(),id.end(),[&](int i,int j){return ca[i]==ca[j]?i<j:ca[i]<ca[j];});

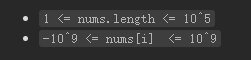
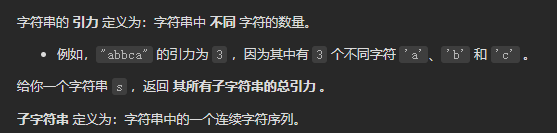
周赛第四题

字符串 计算贡献 dp 字符串的总引力

在字符串结尾添加一个新的字符，实时维护该字符上一次出现的下标；新字符对总引力值的贡献就是当前下标减去上一次出现的下标；若该字符还没有出现，则当前字符的贡献就是当前下标+1，+1的原因是考虑当前字符单独一个，也会贡献一个引力值。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
typedef long long ll;
class Solution {
public:
  long long appealSum(string s) {
    int n = s.size();
    vector<int> loc(26,-1);
    ll sum = 0,res = 0;
    for(int i = 0;i<n;++i){
      int c = s[i]-'a';
      if(loc[c]==-1){
        sum+=i+1; 
      }else{
        sum+=i-loc[c];
      }
      loc[c] = i;
      res+=sum;
    }
    return res;
  }
};

241并查集经典题

a吃b，b吃c，c吃a

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
//
// Created by s'c on 2022/5/1.
//
#include "bits/stdc++.h"
using namespace std;
const int MAXN = 200000;
int par[MAXN];
int ran[MAXN];
int N,K,a,b,c;
void init(int n){
    for(int i = 1;i<=n;++i){
        par[i] = i;
        ran[i] = 0;
    }
}

int find(int x){
    if(x==par[x]) return x;
    else return par[x]=find(par[x]); // 返回时更改节点的父节点为祖宗节点，就是路径压缩操作
}

void unite(int x,int y){
    int fx = find(x);
    int fy = find(y);
    if(fx==fy) return;
    if(ran[fx]<ran[fy]){
        par[fx] = fy;
    }else{
        par[fy] = fx;
        if(ran[fx]==ran[fy]) ran[fx]++;  // 这个优化有的题目会卡
    }
}

int main(){
    cin>>N>>K;
    int res = 0;
    init(3*N);
    while(K-->0){
        scanf("%d%d%d",&a,&b,&c);
        if(b>N||c>N){
            res++;
            continue;
        }
        if(a==2 && b==c){
            res++;
            continue;
        }
        if(a==1){ // bc同一类
            if(find(b)==find(c+N) || find(b)==find(c+2*N)){
                res++;
                continue;
            }
            unite(b,c);
            unite(b+N,c+N);
            unite(b+2*N,c+2*N);
        }else if(a==2){
            if(find(b)==find(c)||find(b)==find(c+N)){
                res++;
                continue;
            }
            unite(b+N,c);
            unite(b+2*N,c+N);
            unite(b,c+2*N);
        }
    }
    printf("%d\n",res);
}

注意

  1. 必须要路径压缩，差距会非常大，即 find(x) 中 return par[x] = find(par[x]);
  2. 可以进行rank优化，会更快一些

5/2

c++不要使用字符加字符串 ‘a’+”asdfa” 超级慢

5/3

二分图判定c++ 二着色问题

问题连接

https://www.papamelon.com/problem/242

学习的地方：

  1. 以EOF结束输入的方法 scanf(); 因为是按位取反，而EOF=-1，补码表示是11111.
  2. c++存图方式，虽然是最垃圾的，vector G[MAX],若有权值或者其他信息，则
1
2
3
4
5
struct edge{
  int to;
  int cost;
  };
vector<edge> G[MAX];

思路

创建一个邻接矩阵，一个color数组表示该节点被染成了什么颜色。由于只有两种颜色，故使用1与-1表示。

  1. dfs函数中，首先将节点染色，然后遍历该节点的邻接表，如果邻接节点染的颜色与本节点相同，则return false；如果邻接节点与本节点染色相反，则直接搜索下一个节点；如果邻接节点没有染色，
    则将邻接节点染成相反的颜色。并且对dfs做判断，if(!dfs(下一个节点,-c)) return false; 之前也遇到过这个技巧，如果dfs返回true不要着急返回true，而是要判断所有的情况都return true才可以。
  2. 主函数中，由于给出的图可能不是联通图，故要使用for循环遍历一下，并判断color[i]有没有染色。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
  //
// Created by s'c on 2022/5/3.
//
#include "bits/stdc++.h"
using namespace std;
const int MAX = 1010;
int n,x,y;
vector<int> G[MAX];
int color[MAX]={0};

bool dfs(int k,int c){
    color[k] = c;
    for(int i = 0;i<G[k].size();++i){
        int to = G[k][i];
        if(color[to]==c) return false;
        if(color[to]==0){ //还没染色
            if(!dfs(to,-c)) return false;
        }
    }
    return true;
}

int main(){
    cin>>n;
    while(~scanf("%d%d",&x,&y)){
        G[x].push_back(y);
    }
    for(int i = 0;i<n;++i){
        if(color[i]==0){
            if(!dfs(i,1)){
                printf("No\n");
                return 0;
            }
        }
    }
    printf("Yes\n");
    return 0;
}

二维差分

image-20220503100257497

5/8

带有剪枝的 状态dfs

我的朴素代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
class Solution {
public:
    bool used[105][105][210]={0};
    bool hasValidPath(vector<vector<char>>& grid) {
        int m = grid.size();
        int n = grid[0].size();
        if(grid[0][0]==')' || grid[m-1][n-1]=='(') return false;
        return dfs(grid,0,0,0);
    }
    bool dfs(vector<vector<char>>& grid,int x,int y,int score){
        int m = grid.size();
        int n = grid[0].size();
        if(score>m-x+n-y-1) return false;
        score += grid[x][y]=='('?1:-1;
        if(score<0) return false;
        if(x==m-1 && y==n-1){
            if(score==0) return true;
        }
        if(used[x][y][score]) return false;
        used[x][y][score] = true;//此点的这个状态已经访问过
        if(x+1<m){
            if(dfs(grid,x+1,y,score)){
                return true;
            }
        }
        if(y+1<n){
            if(dfs(grid,x,y+1,score)){
                return true;
            }
        }
        return false;
    }
};

灵佬的带c++11特性的function函数代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
class Solution {
public:
    bool hasValidPath(vector<vector<char>> &grid) {
        int m = grid.size(), n = grid[0].size();
        if ((m + n) % 2 == 0 || grid[0][0] == ')' || grid[m - 1][n - 1] == '(') return false; // 剪枝
        bool vis[m][n][m + n]; memset(vis, 0, sizeof(vis));
        function<bool(int, int, int)> dfs = [&](int x, int y, int c) -> bool {
            if (c > m - x + n - y - 1) return false; // 剪枝：即使后面都是 ')' 也不能将 c 减为 0
            if (x == m - 1 && y == n - 1) return c == 1; // 终点一定是 ')'
            if (vis[x][y][c]) return false; // 重复访问
            vis[x][y][c] = true;
            c += grid[x][y] == '(' ? 1 : -1;
            return c >= 0 && (x < m - 1 && dfs(x + 1, y, c) || y < n - 1 && dfs(x, y + 1, c)); // 往下或者往右
        };
        return dfs(0, 0, 0);
    }
};

5/9

prim算法思想

一般使用邻接矩阵？？ 邻接表的话，转换成邻接矩阵？？ 还是要分析时间复杂度

与dijkstra算法很类似，都是从某个顶点出发，不断添加边的算法

首先假设有一课只包含一个顶点v的树T，然后贪心地选取T和其他顶点之间相连地最小权值的边，并把它加入到T中，不断进行这个操作，就可以得到一课最小生成树了。

Kruskal算法 使用并查集

Kruskal算法按照边的权值的顺序从小到大查看一遍，如果不产生边（重边也算在内），就把当前这条边加入到生成树中。

第一步就是对边排序

第二步是遍历所有的边

求到某个顶点v的次短路

其实就是二选一

  1. 到某个顶点u的最短路+u v之间的距离
  2. 到某个顶点u的次短路+ u v之间的距离

因此要求的就是源点到每个顶点的最短路和次短路，分别用两个数组dis和dis2来表示

思路

  1. 首先考虑该边能不能更新最短路，如果可以更新最短路就更新，把老的最短路放到次短路上（因为被更新就说明，原来的老的最短路已经不是最短路了，所以把它放到次短路上）；
  2. 若该边不能更新最短路，则考虑用该边更新次短路；若该边不能更新次短路，则不使用该边更新。
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
//
// Created by s'c on 2022/5/9.
//

#include "bits/stdc++.h"
using namespace std;

typedef pair<int,int> P;
int N,R;
const int MAX = 0x3f3f3f3f;
const int LEN =(int)1e5+10;
struct edge{
    int to;
    int cost;
};
vector<edge> G[LEN];

void dijsktra(int tt){
    int dist[5010];
    int dist2[5010];
    priority_queue<P,vector<P>,greater<P>> que;//按照边的权值从小到大排序
    memset(dist,0x3f,sizeof(dist));
    memset(dist2,0x3f,sizeof(dist2));
    dist[1] = 0;
//    dist2[1] = 0;
    que.push(P(0,1));
    while(!que.empty()){
        P p = que.top();
        que.pop();
        int to = p.second;
//        if(dist2[to]<p.first) continue;
        for(int i = 0;i<G[to].size();++i){
            int toto = G[to][i].to;
            int ccost = G[to][i].cost;
            int temp = p.first+ccost;// 注意这里不能写dist[to] 而必须要写p.first，因为此时最短和第二短都会入队，p.first不一定是最短的
//            cout << "p.first=" << p.first << " dist[to]=" << dist[to] << endl;
            if(dist[toto]>temp){
                swap(dist[toto],temp);
                que.push(make_pair(dist[toto],toto));
            }
            if(temp<dist2[toto] && temp>dist[toto]){
                dist2[toto] = temp;
                que.push(make_pair(dist2[toto],toto));
            }
        }
    }
//    for(int i = 1;i<=N;++i){
//        cout << dist2[i] << endl;
//    }
//    cout << "N=" << N << " tt=" << tt << endl;
    printf("%d\n",dist2[tt]);
}

int main(){
    cin>>N>>R;
    for(int i =0;i<R;++i){
        int x,y,D;
        scanf("%d%d%d",&x,&y,&D);
        edge e;
        e.to=y;
        e.cost=D;
        G[x].push_back(e);
        edge e2;
        e2.cost=D;
        e2.to=x;
        G[y].push_back(e2);
    }
//    cout << "完成输入" << endl;
    dijsktra(N);
    return 0;
}

征兵亲密度 最小生成树

题目链接

https://www.papamelon.com/problem/245

思路

可以将题目翻译成求最小生成树的问题

解释一下题意：招募每个人都要花钱，但是若女兵x和男兵y关系好，而且已经招募了其中一个，则招募另外一个的时候，就可以少花一些钱。可以想到的一种思路是，不考虑亲密度，招募所有人需要花费的钱为
10000*(N+M)，而考虑亲密度之后再减去相应的亲密度。为了使付的钱更少，也就是减去的亲密度更多，就需要找亲密度最大的情侣进行征兵。

若将亲密度转化为负数，则找最大亲密度，就相当于找最小的数，就可以利用最小生成树的克鲁斯卡尔算法解决这个问题。

注意，第一次写遇到的问题：

  1. 使用边集数组存储所有的边，然后遍历所有的边，这样使用克鲁斯卡尔算法比窘方便。
  2. 一个关系不需要存储两遍。
  3. 由于男兵女兵都有编号为0，1，2…的人，而女兵有N个，所以不妨让男兵的编号为N+y，这样更方便用并查集解决问题。

其实本质就是贪心的克鲁斯卡尔算法。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
//
// Created by s'c on 2022/5/9.
//
#include "bits/stdc++.h"
using namespace std;
//女N   男M
int T,N,M,R;
int x,y,d;
const int MAX = 20010;
int fa[MAX];
int rrank[MAX];
struct edge{
    int from;
    int to;
    int cost;
};
vector<edge> relation;
bool cmp(const edge&e1,const edge &e2){
    return e1.cost<e2.cost;
}

void init(){
    for(int i = 0;i<MAX;++i){
        fa[i] = i;
        rrank[i] = 0;
    }
}

int find(int x){
    if(x==fa[x]) return x;
    else return fa[x]=find(fa[x]);
}

void merge(int x,int y){
    int fx = fa[x];
    int fy = fa[y];
    if(fx==fy) return;
    if(rrank[fx]<rrank[fy]){
        fa[fx]=fy;
    }else{
        fa[fy]=fx;
        if(rrank[fx]==rrank[fy]){
            rrank[fx]++;
        }
    }
}

bool same(int x,int y){
    return find(x)==find(y);
}

int main(){
    cin>>T;
    while(T-->0){
        relation.clear();
        init();//初始化并查集
        cin>>N>>M>>R;
        int r = R;
        while(R-->0){
            scanf("%d%d%d",&x,&y,&d);
            edge e1,e2;
            e1.from=x;
            e1.to=N+y;
            e1.cost=-d;
            relation.push_back(e1);
        }
        //x   N+y
        int res = 0;
        // 把所有的边排序
        sort(relation.begin(),relation.end(),cmp);

        for(int i = 0;i<r;++i){//遍历所有的边
            edge e = relation[i];
            if(!same(e.from,e.to)){
                merge(e.from,e.to);
                res+=e.cost;
            }
        }
        printf("%d\n",10000*(N+M)+res);
    }
}

5/10

差分约束系统

构造一个有向图，跑SPFA

使用图的思想求解不等式的一组可行解

$x_1-x_2<3$ 则从2到1连一条权值为3的边 终极源点是0 d1-d2<3 d1指从0到1的边的最短距离

从源点0到别的所有点可以连边，也可以不连，连就要都连成一样的数 类似一种基准 求出一种可行解即可，因为通常都不是只有一种解。 可以都初始化成0，因为这样就不用初始化答案数组了，省时省力

最终求从0到所有点的最短距离即可？?？

注意：

  1. 第一次做本题时出错的原因是，建立源点时，源点0到每一个其他点的cost是0没错，但是到其他点的dist不应该是0，而应该是无穷大。因为还是求最短路的思想。

洛谷差分约束系统模板题代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
//
// Created by s'c on 2022/5/11.
//
#include "bits/stdc++.h"
using namespace std;
int n,m;
struct edge{
    int to;
    int cost;
};
vector<edge> G[5010];
queue<int> que;
bool used[5010];//是否在队中
int nums[5010];//入队次数
int dist[5010]={0};// 到源点的最短距离


void spfa(){
    for(int i=1;i<=n;i++) dist[i]=1e9;//最短路，初始值为inf
    dist[0] = 0;
    for(int i = 1;i<=n;++i){
        edge e;
        e.to = i;
        e.cost = 0;
        G[0].push_back(e);
    }
    while(m-->0){
        int a,b,y;
        scanf("%d%d%d",&a,&b,&y);
        edge e;
        e.to = a;
        e.cost = y;
        G[b].push_back(e);
    }

    que.push(0);
    used[0] = true;
    nums[0]++;
    while(!que.empty()){
        int tt = que.front();
        que.pop();
        used[tt] = false;
        for(int i = 0;i<G[tt].size();++i){
            //访问邻接表
            int to = G[tt][i].to;
            int cost = G[tt][i].cost;
//            cout << "访问邻接表了" << endl;
//            cout << "dist[to]=" << dist[to] << " cost=" << cost << endl;
            if(dist[to]>dist[tt]+cost){
                dist[to] = dist[tt]+cost;
//                cout << "进行松弛操作了" << endl;
                if(!used[to]){
                    used[to] = true;
                    nums[to]++;
                    que.push(to);
                    if(nums[to]>=n){
                        printf("NO\n");
                        return;
                    }
                }
            }
        }

    }
    for(int i = 1;i<=n;++i){
        printf("%d%c",dist[i],i==n?'\n':' ');
    }
}
int main(){
    cin>>n>>m;
    spfa();
    return 0;
}

5/13

线段上的格点个数

其实就是求最大公约数

$gcd(|x_1-x_2|,|y_1-y_2|)-1$

区间筛法求素数

之前我们了解过筛法求素数，现在我们思考一下，当面对某个区间$[a,b)$内的数求素数的个数时，要怎么求。

性质1： b以内最小质因数一定不超过$\sqrt(b)$ 。因此筛得$[2,\sqrt(b))$ 中质数的同时，也将其倍数从$[a,b)$ 中抹去。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
//
// Created by s'c on 2022/5/13.
//
#include "bits/stdc++.h"
using namespace std;
typedef long long ll;
ll a,b;
int res = 0;
bool is_prime[1000010]={0};
int primee[1000010]={0}; // [a,b) 区间内的数 是否是素数  下标0代表

int main(){
    scanf("%lld%lld",&a,&b);
    for(int i = 2;1LL*i*i<b;++i){
        if(!is_prime[i]){ // 找到质数
            ll first = (a+i-1)/i*i;
            for(ll j = max(2*i*1LL,first);j<b;j+=i){ // 标记质数的倍数为合数
                int id = (int)(j-a);
                primee[id] = 1;
            }
        }
    }
    for(int i = 0;i<(int)(b-a);++i){
        if(!primee[i]) res++;
    }
    printf("%d\n",res);
    return 0;
}

求大于a的第一个能被i整除的数

$\frac{a+i-1}{i} \times i$

5/14

Carmichael Numbers（卡迈克尔数）

我们把对任意的$1<x<n$ 都有$x^n \equiv x(mod \quad n)$ 成立的合数 n 称为Carmichael Numbers。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
//
// Created by s'c on 2022/5/14.
//
#include "bits/stdc++.h"
using namespace std;
int n;
typedef long long ll;
ll fastpow(ll a,ll b,ll mod){
    ll res = 1;
    while(b>0){
        if(b%2==1){
            res = (res*a)%mod;
        }
        a = (a*a)%mod;
        b = b>>1;
    }
    return res;
}
bool is_prime(int x){
    for(int i = 2;i*i<x;++i){
        if(x%i==0) return false;
    }
    return true;
}
int main(){
    scanf("%d",&n);
    while(n!=0){
        bool flag = true;
        if(is_prime(n)) flag = false;
        for(int x = 2;flag && x<n;++x){
            ll t1 = fastpow(x,n,n);
            if(t1!=x*1LL){
                flag = false;
                break;
            }
        }
        if(flag){
            printf("The number %d is a Carmichael number.\n",n);
        }else{
            printf("%d is normal.\n",n);
        }
        scanf("%d",&n);
    }
//cout << fastpow(2,17,17) << endl;
//cout << fastpow(3,17,17) << endl;
//cout << fastpow(4,17,17) << endl;
//cout << fastpow(5,17,17) << endl;
//cout << fastpow(6,17,17) << endl;
//cout << fastpow(7,17,17) << endl;
//cout << fastpow(8,17,17) << endl;
//cout << fastpow(9,17,17) << endl;
//cout << fastpow(10,17,17) << endl;
//cout << fastpow(11,17,17) << endl;
//cout << fastpow(12,17,17) << endl;
//cout << fastpow(13,17,17) << endl;
//cout << fastpow(14,17,17) << endl;
}

往 ll 上加 int时，要格外注意

1
2
3
4
ll res = 0;
for(int i = 0;i<n;++i){
    res+=1LL*v1[i]*v2[n-i-1];
}

  1. 必须$\times $ 1LL!!!!!!!!!!!!!

  2. 在printf时，一定要 %lld !!!!!!!!!!

疯狂矩阵

题目连接

https://www.papamelon.com/problem/254

主对角线：从左上，到右下
暂且考虑一下最后应该把哪一行交换到第1行。最后的第一行应该具有00…00或者10…00的形式。可以交换到第一行的行当然也可以交换到第2及以后的行。当有多个满足条件的行时，选择离第1行近的行对应的
最终费用要小。这点可以证明。

注意

  1. 需要先预处理出 每一行内最后一个1的位置，0 - n-1
  2. 在交换时，不要交换实际矩阵的值，而是要交换lasto数组的值。因为在交换的过程中用不到实际矩阵。如果要交换实际矩阵，则每次交换后还要重新预处理lasto数组，白白增加了复杂度。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
//
// Created by s'c on 2022/5/14.
//
#include "bits/stdc++.h"
using namespace std;
int T,n;
int g[45][45];
int lasto[45];

int main(){
    scanf("%d",&T);
    int index = 1;
    while(index<=T){
        scanf("%d",&n);
        int res = 0;
        for(int i = 0;i<n;++i){
            for(int j = 0;j<n;++j){
                scanf("%d",&g[i][j]);
            }
        }

        // 预处理每一行最后一个1的位置
        for(int i = 0;i<n;++i){
            int pos = -1;
            for(int j = 0;j<n;++j){
                if(g[i][j]==1){
                    pos = j;
                }
            }
            lasto[i] = pos;
        }

        for(int i = 0;i<n;++i){
            int pos = -1;
            for(int j = i;j<n;++j){
                if(lasto[j]<=i){
                    pos = j;
                    break;
                }
            }
            //交换
            for(int j = pos;j>i;--j){
                swap(lasto[j],lasto[j-1]);
                res++;
            }
        }
        printf("Case #%d: %d\n",index,res);
        index++;
    }
}

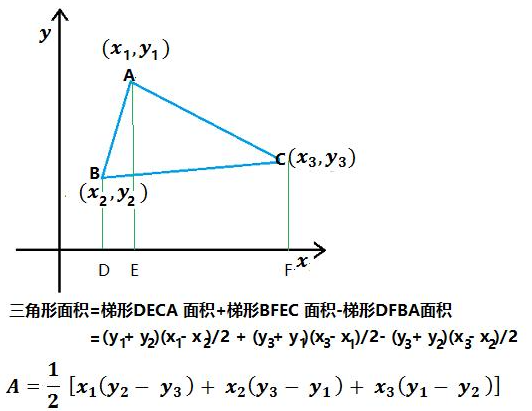
5/15

已知三角形三个顶点，求面积

注意加绝对值

注意数量级

$2 \times 10^5$ 意思是 2后面有5个0

5/27

小数二分

通常使用二分法，check函数O(n),二分O(logn) 总体O(nlog n)

问题连接

https://www.papamelon.com/problem/258

思路

常规二分法的思路，使用二分检查结果，check函数复杂度为O(n)。

注意

  1. 选择左右边界时，左边界选取0.0（因为有可能k>长度最大的L），右边界选取最长的绳子的长度。
  2. double类型在二分的时候，不存在+1的概念，每次都是以mid为边界。
  3. 循环结束条件变为循环100次，1次循环可以把区间范围缩小一半，100次循环则可以达到10^(-30)的精度范围，精度范围基本上没有问题。

另外，也可以设置终止条件为(r-l)>EPS这样，指定一个区间的大小。这种情况下，如果EPS取的太小，就有可能因为浮点小数精度的原因导致陷入死循环，需要额外注意。

代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
//
// Created by s'c on 2022/5/27.
//
#include "bits/stdc++.h"
using namespace std;
int n,k;
double mmax = 1.0;
double a[100005];

bool check(double mid){
    int res = 0;
    for(int i = 0;i<n;++i){
        res+=(int)(a[i]/mid);
    }
    return res>=k;
}
int main(){
    scanf("%d%d",&n,&k);
    for(int i = 0;i<n;++i){
        scanf("%lf",&a[i]);
        mmax = max(mmax,a[i]);
    }
    double l = 0.0,r = mmax;
    int index = 0;
    while(index++<100){
        double mid = (r+l)/2.0;
        if(check(mid)) l = mid;
        else r = mid;
    }
    printf("%.2f",floor(r*100)/100);
}

最大化最小值问题

最小化最大值问题（

6/8

最大化平均值问题

每个物品的重量为$w_i$ 价值为$v_i$ 从中选出k个物品使得单位重量的价值最大。 并不是选择单位重量价值最大的物品，从高到低

c++自定义优先队列排序

  • 优先队列排序时，建议使用仿函数 在定义的时候使用struct 重载()函数执行符 而且在写仿函数的时候不加()

  • sort自定义排序时，可以使用仿函数（struct，重写()函数执行符），也可以使用普通函数（bool cmp()），使用仿函数必须加()，使用普通函数bool cmp不用加()

==推荐使用仿函数==

使用仿函数自定义优先队列实例

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
//
// Created by s'c on 2022/6/8.
//

#include "queue"
#include "iostream"
using namespace std;
typedef pair<int,int>P;
struct cmp{
    bool operator()(const pair<int,int> &p1,const pair<int,int> &p2){
        if(p1.second*1.0/p1.first<=p2.second*1.0/p2.first) return 1;
        else return 0;
    }
};

struct cmp_sort{
    bool operator()(const int & o1,const int & o2){
        return abs(o1)<abs(o2);
    }
};

bool cmp_sort2(const int& o1,const int& o2){
    return abs(o1)<abs(o2);
}

priority_queue<pair<int,int>,vector<pair<int,int>>, cmp> que;

int main(){
    P p1(2,2),p2(5,3),p3(2,1);
    que.push(p1);
    que.push(p2);
    que.push(p3);
    while(!que.empty())
    {
        P p = que.top();
        cout << p.first << " " << p.second << endl;
        que.pop();
    }
    vector<int> a;
    a.push_back(-3);
    a.push_back(3);
    a.push_back(36);
    a.push_back(53);
    a.push_back(322);
    a.push_back(-93);
    a.push_back(0);
    sort(a.begin(),a.end(),cmp_sort2);
    // sort(a.begin(),a.end(),cmp_sort()); 与之等价
    // sort(a.begin(),a.end(),[](int a,int b)-> bool{return abs(a)<abs(b);}); 也可以使用labmda表达式
    for(auto i:a){
        cout << i << " ";
    }
    
} 
/*
2 2
5 3
2 1
*/

6/9

尺取法

使用尺取法时，while循环的判断条件不要是r<n（右下标小于总数），这样会造成最右边的情况还没有处理，就跳出循环了。

较好的处理方式是：最外层是一个无限循环 break出循环的条件是：确保所有的情况已经处理完毕

7/27

矩形之间的嵌套关系是一个典型的二元关系，二元关系可以用图来建模。

嵌套矩形：求DAG图中不固定起点的最长路径

10/2

把一个数最低位的0变成1 n|(n+1)

把一个数最低位的1变成0 n&(n-1)

11/28

  1. 反转链表 递归 双指针

  2. topk 优先队列 快速排序

  3. 快速排序避免有序情况，可以首先花费o(N)将数组shuffle一下

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    import java.util.Arrays;
    import java.util.Random;

    /**
     * Created by 燃烧杯 on 2018/5/12.
     */
    public class ArrayUtils {

        private static Random rand = new Random();

        public static <T> void swap(T[] a, int i, int j){
            T temp = a[i];
            a[i] = a[j];
            a[j] = temp;
        }

        public static <T> void shuffle(T[] arr) {
            int length = arr.length;
            for ( int i = length; i > 0; i-- ){
                int randInd = rand.nextInt(i);
                swap(arr, randInd, i - 1);
            }
        }

        public static void main(String[] args) {
            Integer[] arr = {1, 2, 3, 4, 5, 6, 7};
            shuffle(arr);
            System.out.println(Arrays.toString(arr));
        }
    }

11/29

  1. 实现LRU 哈希表+双向链表，手写双向链表

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    11
    12
    13
    14
    15
    16
    17
    18
    19
    20
    21
    22
    23
    24
    25
    26
    27
    28
    29
    30
    31
    32
    33
    34
    35
    36
    37
    38
    39
    40
    41
    42
    43
    44
    45
    46
    47
    48
    49
    50
    51
    52
    53
    54
    55
    56
    57
    58
    59
    60
    61
    62
    63
    64
    65
    66
    67
    68
    69
    70
    71
    72
    73
    74
    75
    76
    77
    78
    79
    80
    81
    82
    83
    84
    85
    86
    87
    88
    89
    90
    91
    92
    93
    94
    95
    96
    class LRUCache {
        class LinkedNode{
            int key;
            int val;
            LinkedNode pre;
            LinkedNode next;
            public LinkedNode(int _key,int _val){
                this.key = _key;
                this.val = _val;
                this.pre = null;
                this.next = null;
            }
        }
        int size;
        int capacity;
        Map<Integer,LinkedNode> map = new HashMap<>();
        LinkedNode head;
        LinkedNode tail;
        public LRUCache(int c) {
            capacity = c;
            size = 0;
            head = new LinkedNode(0,0);
            tail = new LinkedNode(0,0);
            head.next = tail;
            tail.pre = head;
        }
        
        public int get(int key) {
            if(map.get(key)!=null){
                //存在 返回关键字的值
                // 将该节点移到双向链表头部
                LinkedNode node = map.get(key);
                moveToHead(node);
                return node.val;
            }
            else{
                // 不存在 返回-1
                return -1;
            }
        }
        
        public void put(int key, int value) {
            if(map.get(key)!=null){
                // 存在 更新值 
                // 将该节点移到双向链表头部
                LinkedNode node = map.get(key);
                node.val = value;
                moveToHead(node);
            }
            else{
                // 不存在 直接插入
                // 移到头部
                // 容量超过，则删除尾部节点
                LinkedNode node = new LinkedNode(key,value);
                map.put(key,node);
                addToHead(node);
                size++;
                if(size>capacity){
                    LinkedNode myTail = removeTail();
                    map.remove(myTail.key);
                    size--;
                }
            }
        }
        public void moveToHead(LinkedNode node){
            // 删除该节点
            removeNode(node);
            // 在头部插入该节点
            addToHead(node);
        }
        public LinkedNode removeNode(LinkedNode node){
            node.pre.next = node.next;
            node.next.pre = node.pre;
            return node;// ?????
        }
        public void addToHead(LinkedNode node){
            node.next = head.next;
            node.pre = head;
            head.next = node;
            node.next.pre = node;
        }
        public LinkedNode removeTail(){
            // 要返回删除的节点，因为程序中要删除map中的键值对
            LinkedNode node = tail.pre;
            node.pre.next = tail;
            tail.pre = node.pre;
            return node;  
        }
    }

    /**
     * Your LRUCache object will be instantiated and called as such:
     * LRUCache obj = new LRUCache(capacity);
     * int param_1 = obj.get(key);
     * obj.put(key,value);
     */

12/2

红黑树原理

  1. （根属性）红黑树根节点必须是黑色
  2. 红色节点的孩子必须是黑色的。也就是说，不能由连续的红色节点；两个黑色的节点可以连接一起，也就是说，黑色节点的孩子可以是黑色（红属性）
  3. 红黑树把null作为叶子节点，AVL树不算null节点。（黑属性），任意一个节点，到它的叶子节点的所有路径，包含相同数目的黑色节点。
  4. 整棵红黑树的高度不超过 $2 log_2(n+1)$，n为节点个数

黑色高度（black height）：从一个节点到他的叶子，经过的黑色节点数目，就叫做它的黑色高度

红黑树插入情景

插入节点必须是红色节点

  1. 所插入的红黑树为空节点，则直接插入，并将红色节点染黑。

  2. 所插入的节点key已经存在，则将插入节点的value赋值给存在的节点，进行节点值更新。

  3. 所插入的节点的父节点是黑色，则直接插入即可。

  4. 所插入的节点的父节点是红色，

    1. 情景4.1 叔叔节点存在且为红节点

      将所插入节点称为x，则x的爸爸是红色。根据红黑树的性质（根节点一定是黑色），x一定存在一个爷爷节点，且爷爷节点是黑色。

      处理步骤：

      1. 将x的爸爸和叔叔节点改为黑色
      2. 将x的爷爷节点改成红色
      3. 将x的爷爷节点设置为当前节点，进行后续处理

      可以看到，如果x的爷爷节点的父节点是黑色，那么无需再做任何处理；但是如果x的爷爷节点是红色，则需要将x的爷爷节点设为当前节点，继续尽心插入操作自平衡处理，直到平衡为止。

    2. 情景4.2 叔叔节点不存在 或者叔叔节点为黑色节点，并且插入节点的父节点（P）是祖父节点（PP）的左子节点

      1. 情景4.2.1 插入节点x是父节点（P）的左子节点 （LL双红）
        1. 将父节点P染黑，祖父节点PP染红
        2. 将祖父节点右旋
      2. 情景4.2.2 插入节点x是父节点（P）的右子节点（LR双红）
        1. 将父节点P左旋
        2. 处理LL双红的情况

    3. 情景4.3 叔叔节点不存在或为黑色节点，并且插入节点的父亲节点P是祖父节点PP的右子节点

      1. 情景4.3.1 新插入节点x是父节点P的右子节点（RR双红）
        1. 将插入节点x的父亲节点染黑，祖父节点PP染红
        2. 然后将祖父节点左旋
      2. 情景4.3.2 新插入节点x是父节点P的左子节点（RL双红）
        1. 将父节点P右旋
        2. 处理RR双红的情况

12/7

删除链表

  1. 一般来讲，需要删除头节点，创建一个dummy node 头节点是比较合适的。
    • 不需要删除头节点的题目，就没有必要创建dummy node
  2. 删除链表中的节点，一般需要定位到目标节点的上一个节点
    • 但若不能定位到上一个节点，脑筋急转弯，将下一个节点的值复制到本届点，然后删除下一个节点（保证目标节点不是尾节点）

12/8

  1. JDK1.7源码中，求大于等于一个数的最小2次幂

    1
    2
    3
    4
    5
    6
    7
    8
    9
    10
    int ans = 8;
    int i = (ans-1)<<1;
    i |= i>>1;
    i |= i>>2;
    i |= i>>4;
    i |= i>>8;
    i |= i>>16;
    int res = i - (i>>>1);

    System.out.println(res);  //8

12/10

赋值语句

A=B A有了新的值 是B

3/13

分割字串：相邻元素之间加逗号

#学习记录
算法学习记录
http://example.com/2023/12/05/算法学习记录/
作者
dutsc
发布于
2023年12月5日
许可协议